Problem H: Ether Geometry

Euclid, dwelt in Alexandria, still being convinced firmly that there is no Royal Road to Euclidean Geometry yet, began to feel gradually, reading newspaper articles, watching TV programs, or brainwashed by young students, that it might be possible to create such a discipline as e-Geometry or Geometry on the Internet. In an e-Geometry environment, he could timely discuss geometry issues with many friends of his including Pythagoras, or he could upload new versions of his unparalleled famous archive "Elements of Geometry (Stoicheia)" on his WWW site. He instantly made up his mind to join the Internet.

He started laying ether cable himself from the hub to his terminal in his uniquely shaped study. He designed the cable route as short as possible.

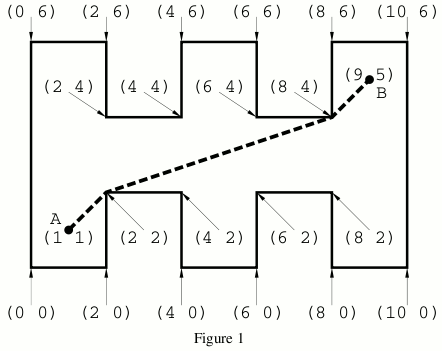
Figure 1 is a plan of his study. Integers in a pair of parentheses like (0 0) are x- and y-coordinates of the nearest pillar or hub or terminal. Between two adjacent pillars are walls indicated by the solid lines. Suppose A is the position of the hub and B his terminal, then the shortest cable may run as drawn with a broken line.

Your mission is to answer the sequence of the coordinates of turning points of the shortest cable route including those of both ends A and B for each plan. So, you are to answer as:

(1 1) (2 2) (8 4) (9 5)

for the example of Figure 1.

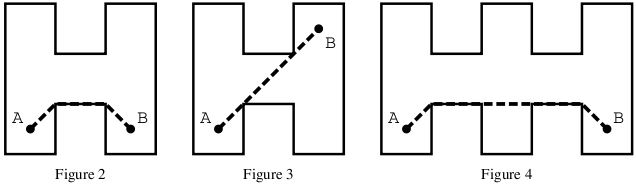
Remember, however, that this is a house of Euclid, the founder and master of Euclidean Geom- etry. The pillars, hub and terminal are ideal points of Euclidean Geometry. The walls and cable are line segments in the sense of geometry. Accordingly, the cable may overlap the walls or the pillars. Hence for Figures 2, 3 and 4, the answers should be as follows:(Hereafter, the layouts of the study are given by means of the lists of the pillar coordinates.)

Figure 2: Pillars:
(0 0) (2 0) (2 2) (4 2) (4 0) (6 0) (6 6) (4 6) (4 4) (2 4) (2 6) (0 6)
Hub: (1 1), Terminal: (5 1)
The answer: (1 1) (2 2) (4 2) (5 1)

Figure 3: Pillars:
(0 0) (2 0) (2 2) (4 2) (4 0) (6 0) (6 6) (4 6) (4 4) (2 4) (2 6) (0 6)
Hub: (1 1), Terminal: (5 5)
The answer: (1 1) (5 5)
Warning: (2 2) (4 4) are not the turning points.

Figure 4: Pillars:
(0 0) (2 0) (2 2) (4 2) (4 0) (6 0) (6 2) (8 2) (8 0) (10 0) (10 6) (8 6)
(8 4) (6 4) (6 6) (4 6) (4 4) (2 4) (2 6) (0 6)
Hub: (1 1), Terminal: (9 1)
The answer: (1 1) (2 2) (8 2) (9 1)

All values of coordinates are integers. Walls are parallel to either x- or y-axis. Walls turn right or left at each pillar for which the coordinates are given. The coordinates of the pillars are given in the order to look the inside of study to the left. From the last pillar in the list, the next wall stretches to the first pillar. Every position of the pillar appears only once in the list. Each pillar is connected to exactly two walls, one of which is parallel to x-axis and the other to y-axis. The whole wall surrounds the study with single stroke closing line. No walls cross. No wall branches exist. It is known that no independent walls or other obstacles are found inside the study. Only one hub and one terminal exist inside the study for each plan, and their positions are always different.

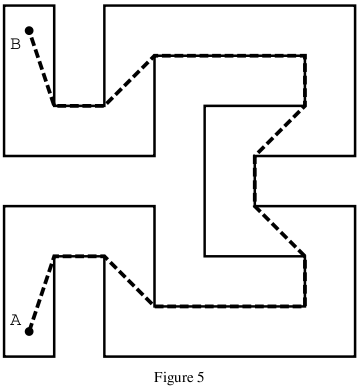
Submit your program when it could solve for the study of complicated shape like Figure 5. This layout is included in the sample input.

Pillars:
(0 0) (2 0) (2 4) (4 4) (4 0) (14 0) (14 6) (10 6) (10 8) (14 8) (14 14)
(4 14) (4 10) (2 10) (2 14) (0 14) (0 8) (6 8) (6 12) (12 12) (12 10)
(8 10) (8 4) (12 4) (12 2) (6 2) (6 6) (0 6)
Hub: (1 1), Terminal: (1 13)
The answer: (1 1) (2 4) (4 4) (6 2) (12 2) (12 4) (10 6) (10 8) (12 10) (12 12)
(6 12) (4 10) (2 10) (1 13) 

Input

The input contains one or more data sets of the coordinates of the pillars, hubs and terminals. Each set begins with a line of an integer n (4 ≤ n ≤ 208), which is the number of the pillars of the study. The following lines contain the coordinates of pillars, five pairs of coordinates per line. After these lines comes one line that contains the coordinates of the hub (a_x a_y) and the terminal (b_x b_y).

The structure of one complete data set is as follows:(Input/output data do not use parentheses.)

n 						
x1 y1 x2 y2 ... x5 y5
x6 y6 x7 y7 ... x10 y10
x11 y11 ...
        ... xn yn ...
ax ay bx by

To make the situation simple, the coordinates of the pillars are all even integers, while those of the hub and terminal are all odd. It is also known that the room size is less than 100 coordinate units in both x and y directions and the cable length is shorter than 1000 coordinate units.

The input is terminated by a line having one 0 after the last set.

Output

For each data set, print the sequence of the coordinates of turning points of the shortest cable with those of the hub at the beginning and those of the terminal at the end. Each line should contain five pairs of coordinates separated by a single space, except the last of these lines which may contain fewer than five. In each coordinate pair, x and y values should be separated also by a single space. The last coordinate of each line may be followed by a single space. The answer of each data set must be followed by a single empty line.

Sample Input

The sample input corresponds to Figures 1 and 5.

20
  0  0  2  0  2  2  4  2  4  0
  6  0  6  2  8  2  8  0 10  0
 10  6  8  6  8  4  6  4  6  6
  4  6  4  4  2  4  2  6  0  6
  1  1  9  5
 28
  0  0  2  0  2  4  4  4  4  0
 14  0 14  6 10  6 10  8 14  8
 14 14  4 14  4 10  2 10  2 14
  0 14  0  8  6  8  6 12 12 12
 12 10  8 10  8  4 12  4 12  2
  6  2  6  6  0  6
  1  1  1 13
 0

Output for the Sample Input

1 1 2 2 8 4 9 5

1 1 2 4 4 4 6 2 12 2
12 4 10 6 10 8 12 10 12 12
6 12 4 10 2 10 1 13

---