Problem J: Avant-garde Art
ICPC World Finals 6日目
ロシア構成主義とは、1910年代半ばに始まったソ連における芸術運動である。 R国に長く滞在していたティー氏は、 そのようなものに感化され、 ICPC World Finalsのリハーサル中にも関わらず、 クールなデザインを作ることにした。 ティー氏は語る: 「記号は円と線分だけで充分だ。 線分をいかに美しく交差させるかが重要である。」
問題
円周に\(n\)個の座標\( 1, 2, …, n \)を等間隔に割り当てる。 各座標からはちょうど1本の線分が出ており、 座標\( i \)の線分は異なる座標\( a_{i} \)に結ばれている。 (逆に、座標\( a_{i} \)の線分は座標\( a_{a_{i}} = i \)に結ばれている。) この状態から高々\( k \)本の線分を(座標・長さに関係なく自由に)円周上に結び直すことが出来る。 互いに交差している線分の集合の最大サイズを答えよ。
入力
n k a1 a2 … an
1行目に座標の数\(n\)、結び直すことのできる線分の数\(k\)が空白区切りで与えられる。 2行目に座標\(i\)の線分が結ばれる座標を表す\( a_{i} \)が空白区切りで与えられる。
出力
高々\(k\)本の線分を結び直した後に 互いに交差している線分の集合の最大サイズを1行に出力せよ。
制約
- \( 2 \leq n \leq 8000 \)
- \(n\)は偶数
- \( 0 \leq k \leq \min(n/2, 20) \)
- \( 1 \leq a_{i} \leq n \)
- \( a_{i} \not = i \)
- 線分を自分自身に結ぶことは無い
- \( a_{i} \not = a_{j} (i \not = j) \)
- 同じ座標に2本以上の線分が結ばれることは無い
- \( a_{a_{i}} = i \)
- \(i\)から\(j\)に線分が結ばれているならば、\(j\)から\(i\)に線分が結ばれている
入出力例
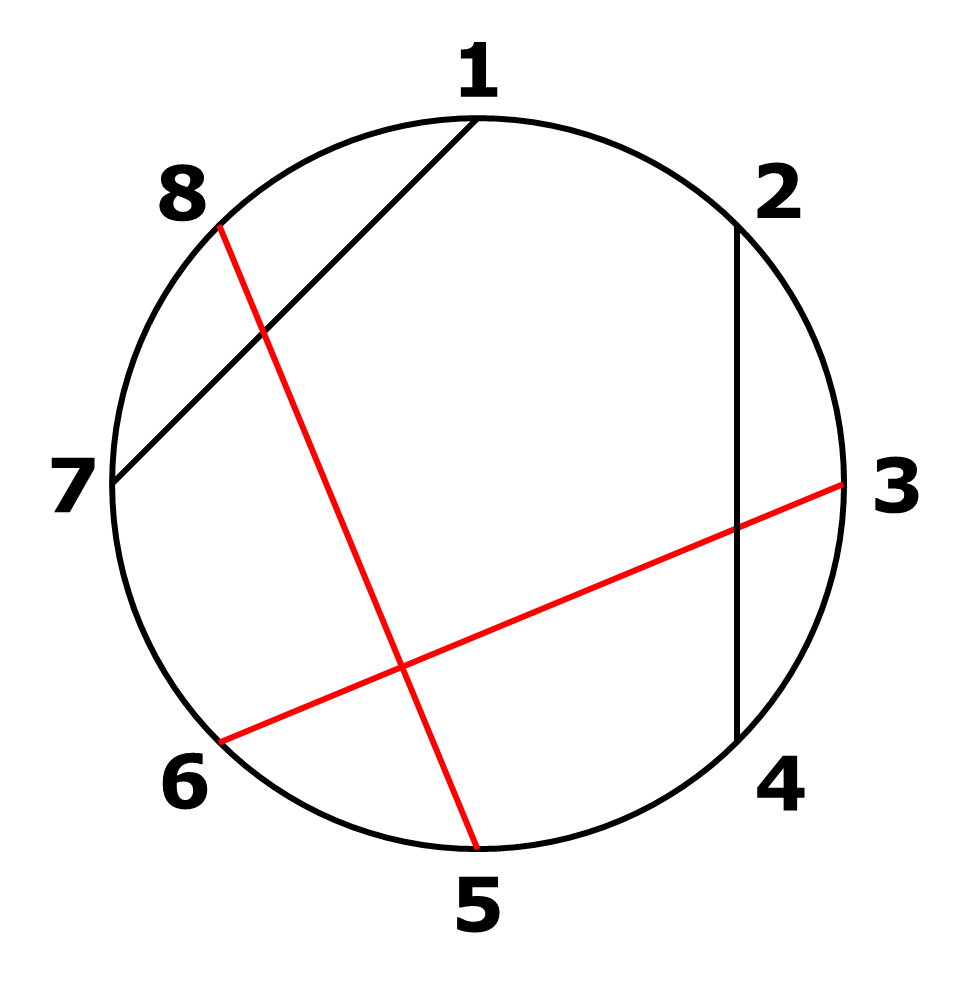
入力1
8 0 7 4 6 2 8 3 1 5
出力1
2
互いに交差する線分は下図の赤い線分で表される。
入力2
8 1 7 4 6 2 8 3 1 5
出力2
3
1,7を結ぶ線分を下図のように結び直せば互いに交差する3つの線分が得られる。

入力3
8 0 5 6 7 8 1 2 3 4
出力3
4
全ての線分は互いに交差しているため、交差する最大の線分の数は4となる。
