G - 自由研究
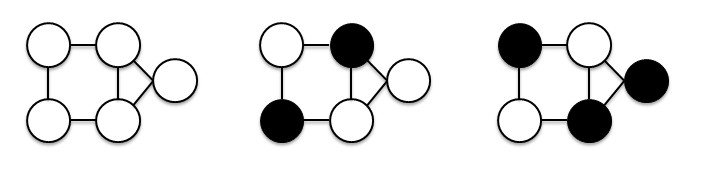
きつねの次郎は夏休みの自由研究で最大独立集合問題のアルゴリズムを考えている. 最大独立集合問題では,入力として無向グラフ G=(V,E) が与えられる. G の各頂点が白または黒で塗られており,どの辺の端点も少なくとも一方が白く塗られているとき,黒い頂点集合のことを独立集合と呼ぶ. 例えば下図において,図の左部のようなグラフが与えられた時,図の中央部のように色を塗ると黒い頂点集合は独立集合になっているが,一方で図の右部のように色を塗った場合は黒い頂点集合は独立集合になっていない. 問題の目的は,要素数が最大であるような独立集合を求めることである. 便宜上,グラフ G の最大の独立集合の大きさを A(G) と記す.
残念ながらこの問題はNP困難であることが知られており,多項式時間で最適値を求めることは多分できそうにない. そこで,きつねの次郎は理論的には保証がないがなんとなくうまくいきそうな乱択アルゴリズムを考案した.そのアルゴリズムは次のようなものである.
【次郎のアルゴリズム】N=|V| をグラフの頂点数とする. 最初,すべての頂点は白で塗られている. いま,各頂点に 1,2,…,N の番号を,どの2つの頂点も互いに異なる番号を持つように割り当てる. このとき,N! = N \times (N-1) \times (N-2) \times … \times 1 通りの割り当て方が存在するが, これらの中から一様な確率で無作為に割り当てるものとする. 各頂点 v について,もし v に隣接するすべての頂点 w に対して v に割り当てられた番号が w より小さいとき v を黒く塗るということをする. (もし v に隣接する頂点が存在しない場合,アルゴリズムは v を黒く塗るものとする.) そして,黒く塗られた頂点を,問題の解として出力する.
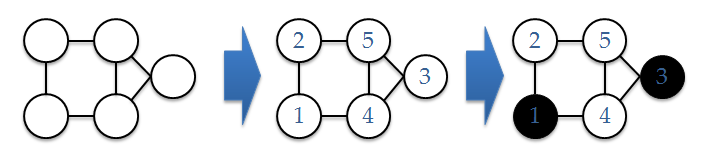
次郎のアルゴリズムの動作例を下図に示す. 図の左部のようなグラフが与えられたとき,各頂点に番号を(無作為に)割り当て,そこから条件を満たす頂点を黒く塗っている.
定義から,このアルゴリズムによって黒く塗られる頂点集合は独立集合になっていることがわかる. アルゴリズムを作り,すっかり自信に満ちた様子の次郎であったが,それを横から見ていたきつねのしえるが突っ込みを入れてきた. そんなアルゴリズムでは全然良い解は出ない,と. 納得しようとしないきつねの次郎にために,しえるは致命的なケースを見せることにした.
E(G) を次郎のアルゴリズムが出力する黒い頂点集合の大きさの期待値とする. 頂点数が40以下の無向グラフで,A(G)-E(G) が最大になるようなものを1つ作り,それを出力せよ.
入力形式
入力は無い.
出力形式
題意を満たすグラフを出力せよ. グラフの出力形式は以下に従うものとする.
N
s_{11}s_{12}s_{13}…s_{1n}
s_{21}s_{22}s_{23}…s_{2n}
s_{31}s_{32}s_{33}…s_{3n}
…
s_{n1}s_{n2}s_{n3}…s_{nn}
n はグラフの頂点数である.
s_{ij} はグラフの接続関係を表す文字である.
頂点 i と j の間に辺が無いとき s_{ij}=N であり,
頂点 i と j の間に辺が有るとき s_{ij}=Y であるものとする.
制約とグラフの性質から,以下の条件を満たさなければならない.
- 1 ≤ N ≤ 40
- s_{ii} =
N - s_{ij} = s_{ji}
入出力例
以下に入出力例を示すが,問題の性質上,最適解の出力を記すことはできないので,ここでは出力形式を満たす最適ではない解の例を示す.
入力例 1
出力例 1
3 NYY YNY YYN
この出力は 3 頂点の完全グラフを表す.このグラフでは A(G) = E(G) = 1 であり,致命的なケースには程遠い.
入力例 2
出力例 2
3 NYN YNY NYN
この出力は 3 頂点のパスグラフを表す.このグラフでは A(G) = 2,E(G) = (1+1+1+1+2+2)/6 = 4/3 なので, A(G) - E(G) = 2/3 となる.