挿入ソート
挿入ソートでは図のように、各計算ステップにおいて、配列は「ソート済みの部分列」と「未ソートの部分列」の2つの部分列に分けられます。
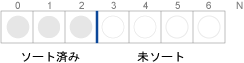
挿入ソート
- 先頭の要素をソート済みとする。
- 未ソートの部分がなくなるまで、以下の処理を繰り返す:
1. 未ソート部分の先頭から要素を1つ取り出し $v$ に記録する。
2. ソート済みの部分において、$v$ より大きい要素を後方へ1つずつ移動する。
3. 最後に空いた位置に「取り出した要素 $v$」を挿入する。
例えば、配列 8, 3, 1, 5, 2, 1 に対して挿入ソートを行うと以下のようになります。
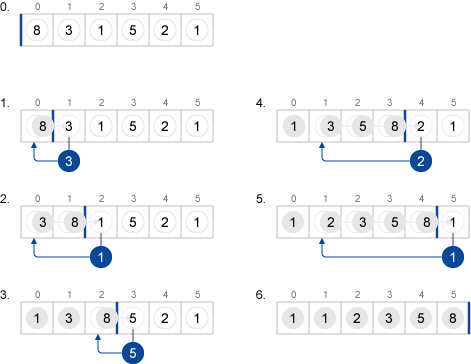
1. では先頭の要素 A[0] (=8)はソート済みであり、A[1] の3を取り出しソート済み部分列の適切な位置に挿入します。まず、A[0]にあった8をA[1]に移動してから、A[0]に3を挿入します。これにより、最初の2つの要素がソート済みとなります。
2. では、A[2]の1を適切な位置に挿入します。まず、1より大きいA[1] (= 8)とA[0](= 3)をこの順番で後方へ1つ移動し、A[0] に1 を挿入します。
3. では、A[3] の5を適切な位置に挿入します。5より大きいA[2](=8)を後方へ1つ移動し、A[2] に5を挿入します。
以降同様に、ソート済みの部分列の一部を後方へ移動し、未ソートの部分列の先頭の要素を、ソート済み部分列の適切な位置に挿入していきます。挿入ソートでは、0 から $i$ 番目の要素がソート済みの部分列のとき、入力として与えられた数列の 0 から $i$ 番目の要素がソート済みとなる状態が常に保たれます。
挿入ソートの実装に必要な主な変数は以下のようになります。
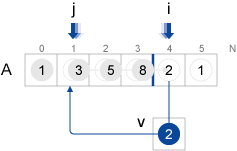
| A[N] | サイズがNの整数型配列。 |
| i | 未ソートの部分列の先頭を示すループ変数。 |
| v | A[i]の値を一時的に保持しておくための変数。 |
| j | ソート済み部分列からvを挿入するための位置を探すループ変数。 |
外側の繰り返し処理でi を1 からひとつずつ増加させていきます。各繰り返し処理の最初でv にA[i] の値を一時的に保持しておきます。
続く内部の繰り返し処理で、ソート済みの中でv より大きい要素を後ろに1つ移動させます。ここでは、j がi-1 を始点として先頭に向かって減少し、その過程でvより大きいA[j] がA[j+1] へ移動します。j が-1 に達したとき、あるいはA[j] がv 以下となったときに、この繰り返し処理が終了し、このときのj+1 がv を挿入する位置になります。
挿入ソートは離れた要素を直接交換することはなく、取り出した値vより大きい要素のみを後方に移動するので、安定なソートアルゴリズムです。
挿入ソートの計算量を考えてみましょう。ここでは、各$i$のループでA[j] の要素を後方へ移動する回数を見積もります。最悪の場合、$i$ のループの各処理が $i$ 回行われるので、$1 + 2 + ... + N - 1 = (N^2 − N)/2$ となり、$O(N^2)$ のアルゴリズムとなります。このように、オーダーの計算では多くの場合、まず大まかな計算ステップ数を見積もり、求めた式の最も影響のある項を残し、定数を無視することで得られます。例えば、$N^2/2 - N/2$ においては、$N$ は $N^2$ に比べ十分小さいので無視することができ、さらには定数倍の $1/2$ を無視して、おおよそ $N^2$ に比例すると見積もります。このとき、$N$ は十分大きな値であると仮定します。
挿入ソートは、入力のデータの並びが、計算量に大きく影響する興味深いアルゴリズムの1つです。計算量が $O(N^2)$になるのは、データが降順に並んでいる場合です。一方、データが昇順に並んでいる場合は A[j] の移動が必要ないため、おおよそ $N$ 回の比較ですみます。従って、挿入ソートはある程度整列されたデータに対しては高速に動作する特長を持ちます。
Reference

|
プログラミングコンテスト攻略のためのアルゴリズムとデータ構造 (マイナビ)AIZU ONLINE JUDGE のコース問題を題材にした解説書です。初級者が体系的にアルゴリズムとデータ構造の基礎を学ぶことができる入門書となっています。 |