Integral

Write a program which computes the area of a shape represented by the following three lines:

$y = x^2$
$y = 0$
$x = 600$

It is clear that the area is $72000000$, if you use an integral you learn in high school. On the other hand, we can obtain an approximative area of the shape by adding up areas of many rectangles in the shape as shown in the following figure:

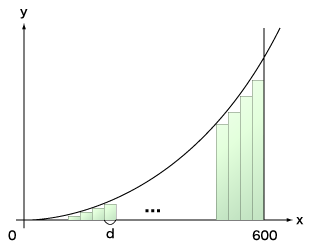
$f(x) = x^2$

The approximative area $s$ where the width of the rectangles is $d$ is:

area of rectangle where its width is $d$ and height is $f(d)$ $+$
area of rectangle where its width is $d$ and height is $f(2d)$ $+$
area of rectangle where its width is $d$ and height is $f(3d)$ $+$
...
area of rectangle where its width is $d$ and height is $f(600 - d)$

The more we decrease $d$, the higer-precision value which is close to $72000000$ we could obtain. Your program should read the integer $d$ which is a divisor of $600$, and print the area $s$.

Input

The input consists of several datasets. Each dataset consists of an integer $d$ in a line. The number of datasets is less than or equal to 20.

Output

For each dataset, print the area $s$ in a line.

Sample Input

20
10

Output for the Sample Input

68440000
70210000

---