苗木
植物学者のサトー博士は苗木用の特殊肥料を何種類も発明しました。その肥料を苗木に与えると、瞬く間に苗木の大きさが変わります。 但し、肥料に以下のように副作用があることが判明しました。
- 1 回目に与えた肥料だけでは、苗木の大きさが変わりません。
- 2 回目以降は、その回に与えた肥料と、その直前に与えた肥料との組み合わせによって苗木に影響を与えます。良い影響を与えると苗木が伸び、悪い影響を与えると苗木が縮んでしまうこともあります。
試しに、サトー博士は 3 種類の肥料 (肥料 1、2、3) に対し、ある時点で与えた肥料 (今回の肥料) とその直前に与えた肥料 (直前の肥料) の組み合わせによる苗木の成長度合いを調べ、以下の「成長度表」を作成しました。
|
右表の 1 行目は今回与える肥料の番号で、1 列目はその直前に与えた肥料の番号です。他の数字は直前に与えた肥料と今回与える肥料の組み合わせによる苗木の成長度 (成長後対成長前の大きさの比率) を示します。成長度 > 1.0 の場合は苗木が伸びる、成長度 < 1.0 の場合は苗木が縮むことを示します。例えば肥料 1 の後に肥料 2 を与えると苗木の大きさが 3 倍になるが、肥料 1 の後に肥料 3 を与えると苗木の大きさが半分に縮んでしまいます。 |
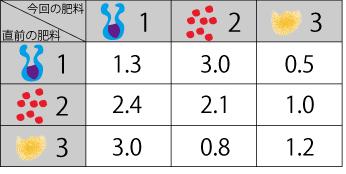
|
苗木に与える肥料の回数が制限された場合、苗木をできるだけ大きく育てるにはどの肥料をどのような順で与えればよいでしょうか?「成長度表」がその答え教えてくれます。例として上の表にある肥料を 3 回だけ与える場合、以下のように肥料 3 → 肥料 1 → 肥料 2 の順にあげると最も苗木が成長します。

- 1 回目の肥料 (肥料 3) では苗木の大きさは変わりません。
- 2 回目の肥料 (肥料 1) では、表より肥料 3 後の肥料 1 での成長度が 3.0 なので、苗木の大きさは前回の 3.0 倍になります。
- 3 回目の肥料 (肥料 2) では、表より肥料 1 後の肥料 2 での成長度が 3.0 なので、苗木の大きさはさらに前回の 3.0 倍で、最初の 3.0 × 3.0 の 9.0 倍になります。
今度は、サトー博士は発明した n 種類の肥料を全部調べて、上のような「成長度表」を作りあげましたが、非常に大きな表になってしまい、肥料の種類と与える順番を決めるのに大変苦労しています。
そこで博士に代わり、n 種類の肥料の組み合わせによる苗木の「成長度表」中の成長度値部分を入力とし、肥料を m 回与えた後の最大の苗木の大きさを求めるプログラムを作成してください。ただし、初めの苗木の大きさを 1 とし、1 回目に与える肥料の成長度はどの肥料でも 1.0 とします。なお、肥料は 1 から n まで番号付けされています。
Input
複数のデータセットの並びが入力として与えられます。入力の終わりはゼロふたつの行で示されます。 各データセットは以下の形式で与えられます。
n m g11 g12 ... g1n g21 g22 ... g2n : gn1 gn2 ... gnn
1 行目に肥料の種類数 n (2 ≤ n ≤ 100)、 肥料を与える回数 m (1 ≤ m ≤ 100) が与えられます。
続くn 行に、肥料 i の後に肥料 j を与えた時の苗木の成長度 gij (0.0 ≤ gij ≤ 10.0, 実数) が与えられます。
データセットの数は 20 を超えません。
Output
データセット毎に、最大の苗木の大きさを1行に出力します。出力する苗木の大きさは、小数点第 3 位を四捨五入して、小数点第 2 位まで求めてください。
Sample Input
3 3 1.3 3.0 0.5 2.4 2.1 1.0 3.0 0.8 1.2 2 2 1.0 1.0 1.0 1.0 0 0
Output for the Sample Input
9.00 1.00