コンビニ

コンビニエンスストア・デブンイレブンは事業を広げるため若松市に一店舗目をオープンしようと考えています。若松市には既に他のたくさんのコンビニエンスストアがあるので、新店舗をオープンする場所が成功の鍵を握ることになりそうです。デブンイレブンは「お客さんは自分の住んでいる地域から最も近いコンビニを利用する」という前提の下、「多くのお客さんが利用するであろう地点」に出店することにしています。

デブンイレブンは、既設の各コンビニがカバーしている範囲を把握するため、若松市の地図を合同な正六角形(以後「ブロック」)を用いて区分しました。このとき、各ブロックには既設のコンビニが多くとも一つだけ入るように区分しました。この地図上で、各ブロックからあるコンビニへ行くのに経由するブロックの数をもとにコンビニとの距離を求めます。各ブロックはこの距離が最も小さいコンビニによってカバーされていると考えます。問題は、この地図をもとに「できるだけ多くのブロックをカバーする既設のコンビニがないブロック」を探すことです。

デブンイレブンのプログラマであるあなたは、ブロック分けされた地図情報と新店舗の候補地の情報から、最も広くカバーできるブロック数を計算するプログラムを開発することになりました。

m × n に区分した地図は図1のように表します。六角形のブロックが横に m 個、縦に n 個並び、それぞれは一つの座標(x, y)で示されます。奇数行の左端はその上の行の左端の左下に、偶数行の左端はその上の行の左端の右下に、それぞれ位置します。例えば、座標(1, 1)は図1の一番左上のブロックを示します。また、座標(1, 2)は座標(1, 1)の右下に位置し、座標(1, 3)は座標(1, 2)の左下に位置します。

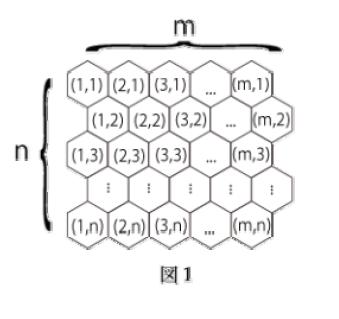
図2は既設のコンビニが6個あった場合の例で、6 × 6 に区分されています。各コンビニは1から順に番号が振られています。このとき、各コンビニがカバーするブロックを番号毎に塗り分けると図3のようになります。座標(1, 4)や(2, 5)のように塗られていないブロックは最も近いコンビニが二つ以上あり、どちらとも判断がつかないブロックになっています。例えば、座標(1, 4)のブロックの場合、番号4のコンビニと番号5のコンビニへの距離が等しく、このブロックをカバーしているコンビニはないものとして考えます。番号4のコンビニがカバーしているブロック数は5となります。

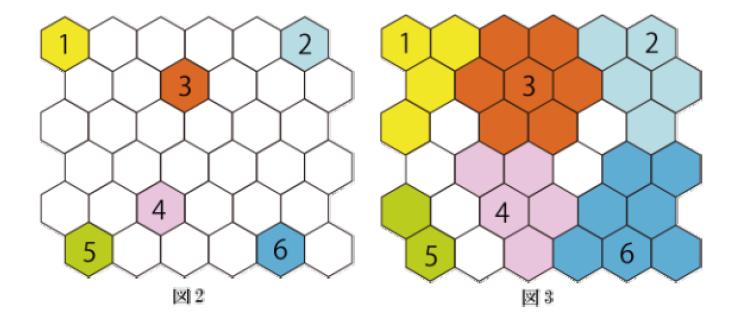
ここで、デブンイレブンが座標(1, 3)と座標(5, 3)を新店舗の候補地として考えているとします。座標(1, 3)に店舗を構えた場合、カバーできるブロック数は3となります(図4)。一方、座標(5, 3)に店舗を構えた場合にカバーできるブロック数は4となります(図5)。したがって、最も広くカバーできるブロック数は4となります。

地図情報 m × n、既設のコンビニの数 s とその座標(x, y)、候補地の数 t とその座標(p, q)を入力とし、全候補地の中で最も広くカバーできるブロック数を出力するプログラムを作成してください。

Input

複数のデータセットの並びが入力として与えられます。入力の終わりはゼロふたつの行で示されます。 各データセットは以下の形式で与えられます。

m n
s
x1 y1
x2 y2
:
xs ys
t
p1 q1
p2 q2
:
pt qt

1 行目に区分した地図の大きさ(横、縦)を表す整数 m, n (2 ≤ m, n ≤ 100) が与えられます。

2行目に既設のコンビニの数 s (1 ≤ s ≤ 10) が与えられます。続くs 行に、 i 個目の既設のコンビニの座標 x_i, y₁ が与えられます。

続く行に、新店舗の候補地の数 t (1 ≤ t ≤ 10 ) が与えられます。続く t 行に、i 個目の候補地の座標 p_i, q_i が与えられます。

データセットの数は 20 を超えません。

Output

データセット毎に、全候補地の中で最も広くカバーできるブロック数を１行に出力します。

Sample Input

6 6
6  
1 1
6 1
3 2
3 5
1 6
5 6
2
1 3
5 3
6 6
6
3 2
3 5
6 1
1 1
1 6
5 6
2
2 3
5 3
0 0

Output for the Sample Input

4
4

---