最大公約数-ユークリッドの互除法
最大公約数は、コンピュータ上で扱う数学には欠かせない要素です。最大公約 数を使うことで、計算の効率が大きく変動することもあります。最大公約数を求めるアルゴリズムのひとつが「ユークリッドの互除法」です。その処理 の流れを以下に示します。
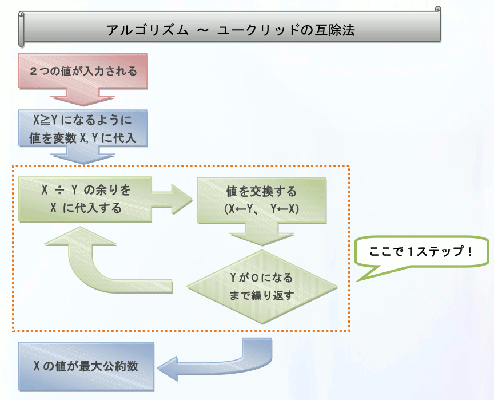
例えば 1071 と 1029 の場合、1071 を X 、1029 を Y に代入して、
1071 ÷ 1029 の余りは 42 、X に 42 を代入して X と Y を入れ替える。 (1 ステップ)
1029 ÷ 42 の余りは 21 、X に 21 を代入して X と Y を入れ替える。 (2 ステップ)
42 ÷ 21 の余りは 0 、X に 0 を代入して X と Y を入れ替える。 (3 ステップ)
Y が 0 になったので、この時の X が最大公約数となる。よって最大公約数は 21 。
このように、たったの 3 ステップで 1071 と 1029 の最大公約数を求めることが出来ました。ユークリッドの互除法は約数を出して比較していく方法に比べ、圧倒的に早く結果を出してくれます。
2つの整数を入力とし、ユークリッドの互除法を用いて最大公約数を求め、その最大公約数と計算にかかったステップ数を出力するプログラムを作成してください。
Input
複数のデータセットの並びが入力として与えられます。入力の終わりはゼロふたつの行で示されます。 各データセットとして2つの整数 a, b (2 ≤ a, b ≤ 231-1) が1行に与えられます。
データセットの数は 1000 を超えません。
Output
データセットごとに、入力された2つの整数の最大公約数と、計算にかかったユークリッドの互除法のステップ数を空白区切りで1行に出力します。
Sample Input
1071 1029 5 5 0 0
Output for the Sample Input
21 3 5 1