迷子の双子

たかゆき君とかずゆき君は仲良しの双子ですが、行動が真逆です。 例えば、たかゆき君が西に行けば、かずゆき君は東へ行き、かずゆき君が北へ行けば、たかゆき君は南へ行きます。 現在 2 人はデパートに来ており、別々の場所にいます。真逆に移動してしまう 2 人ができるだけ早く出会うためにはどうしたらよいでしょうか?

デパートは横 W 個 × 縦 H 個のマスで構成されるグリッドで表され、2 人は単位時間に東西南北に 1 マス分移動することができます。ただし、グリッドの範囲外や障害物のあるマスに移動することはできません。

図のように、グリッドのマスの位置は座標 (x, y) で表されます。

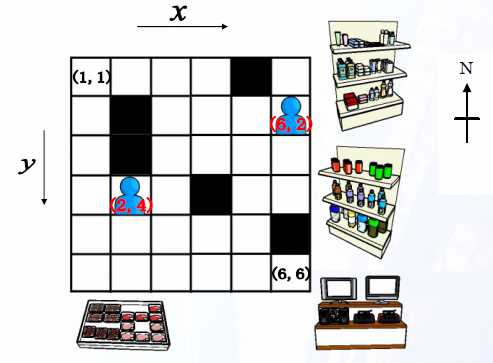
グリッドの情報と 2 人の初期位置を入力とし、2 人が出会うまでの最短の時間を出力するプログラムを作成してください。出会うことができない場合や、出会うのに 100 以上の時間を要する場合は、NA と出力してください。グリッドの情報は、H 行 W 列の数字、2 人の位置情報は座標によって与えられます。

移動後にたかゆき君かかずゆき君のうち、どちらか一方が障害物やグリッドの範囲外に位置してしまうときには、移動ができないので、障害物やグリッドの範囲外に位置する方は元の場所に戻りますが、そうでない方は元の場所に戻ることなく動くことができます。

なお、2 人が出会うとは、移動後に 2 人が同じマスに止まることを言います。2 人がすれ違っても、出会ったことにはなりません。

Input

複数のデータセットの並びが入力として与えられます。入力の終わりはゼロふたつの行で示されます。 各データセットは以下の形式で与えられます。

W H
tx ty
kx ky
d11 d21 ... dW1
d12 d22 ... dW2
:
d1H d2H ... dWH

1 行目にデパートの大きさW, H (1 ≤ W, H ≤ 50) が与えられます。2 行目にたかゆき君の初期位置 tx, ty、3 行目にかずゆき君の初期位置 kx, ky が与えられます。

続く H 行にデパートの情報が与えられます。d_i,j はマス (i, j) の種類を表し、0 のとき移動可能なマス、1 のとき障害物があるマスを表します。

データセットの数は 100 を超えません。

Output

入力データセットごとに、最短の時間を１行に出力します。

Sample Input

6 6
2 4
6 2
0 0 0 0 1 0
0 1 0 0 0 0
0 1 0 0 0 0
0 0 0 1 0 0
0 0 0 0 0 1
0 0 0 0 0 0
3 3
1 1
3 3
0 0 0
0 1 0
0 0 0
0 0

Output for the Sample Input

3
NA

---