人生ゲーム
太郎君は、おもちゃ屋さんに会津ホビー社製の人生ゲームを買いに行きました。人生ゲームは、マス目の書かれたボードとルーレットを使って遊びます。ボードには図のようにスタート地点とゴール地点が一つずつあり、それらはひとつながりのマス目でつながっています。最初に、コマはスタート地点のマスに置かれ、ルーレットを回して出た数によってコマを進めます。マスによっては、そこに止まったり通過したりすることでお金を得たり、コマの位置を変えたりするイベントマスがあります。最終的な勝敗は、コマがゴール地点に到達した時点の所持金の多寡で決まります。
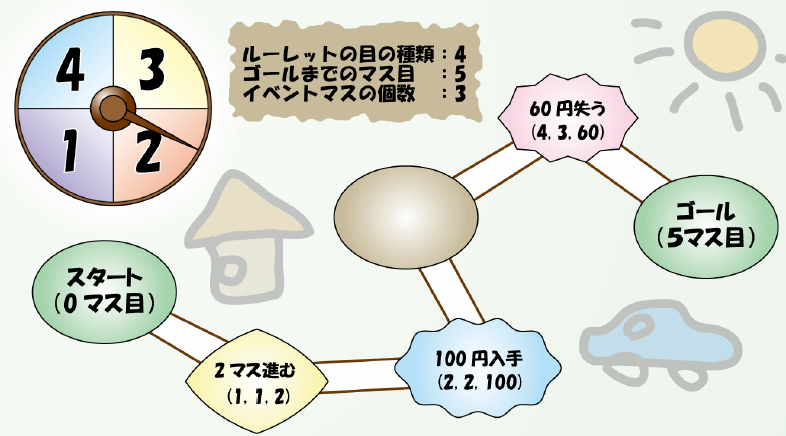
この会社の人生ゲームの面白いところは、ルーレットの出る目の大きさ、ゴールまでのマスの数、イベントマスの配置がひとつひとつパッケージごとに異なるところです。それらはケースに書かれており、それを読むことで確認することができます。お金を最も得られる人生ゲームを選びたい太郎君は、得るお金の期待値が一番大きいものを買いたがっています。そこであなたは、太郎君のゲーム選びを手伝うことにしました。
ルーレットは、円周を X 等分に区分され、それぞれに V1、V2、...、VX という値が記入されているとします。ボードには、0 番、1 番、...、Y 番と番号がふられたマス目があり、順番につながっています。マス目の中には、イベントマスと呼ばれる特別なマスが Z 個あり、そこに到達すると特別な動作を行います。イベントマスのマス目の番号は Ni で与えられます。イベントマスには 1 ~ 3 の種類 (Ei) があり、それぞれ次の動作が行われます。
| 種類 (Ei) | 特別動作 | 値 (Ai) の範囲 |
|---|---|---|
| 1 | 指定の値 Ai だけ先へ進む | 1~10 |
| 2 | 指定の値 Ai の金額を得る | 1~100 |
| 3 | 指定の値 Ai の金額を支払う | 1~100 |
最初の所持金は 0 円で、第 0 マス目からスタートし、第 Y マス目に到達するとゴールとなります。ゴールを越えた場合もゴールと見なします。スタートとゴールにイベントは無く、1 マスに複数のイベントが重なることはありません。イベントによって進んだ先のマスのイベントは無視します。所持金が 0 円より少なくなる場合は 0 円とします。
例えば、ある人生ゲームで得られるお金の期待値は以下のように計算できます。
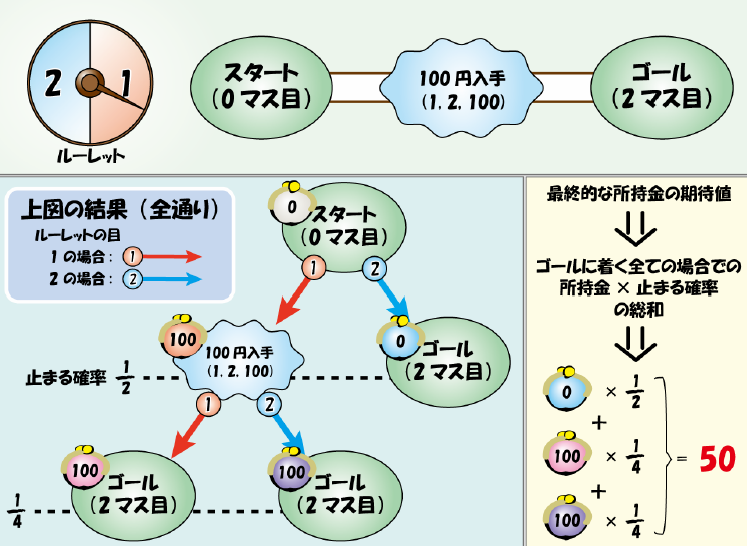
この例では、スタート、イベントマス(100 円入手) 、ゴールの 3 つのマスと、1 か 2 が出るルーレットからなる人生ゲームが表されています。まず、1 回目にルーレットを回した時、1 が出ればイベントマスに到達し、所持金は 100 円になります。一方、2 が出た場合はゴールに到達し、所持金は 0 円のままです。これらはどちらも 2 分の 1 の確率で起こります。
さらに、1 回目でイベントマスに到達した場合は 2 回目のルーレットを回しますが、どの値が出てもゴールに到達し、所持金はどの場合も 100 円です。
このように、全部で 3 通りのゴールの仕方があります。ゴールした時点の所持金に着目すると、0 円になる場合が 1 通りでその確率は 2 分の 1、100 円になる場合が 2 通りでその確率が 4 分の 1 です。この場合、ゴールでの所持金の期待値は、ゴールの仕方ごとの (所持金 × その確率) を足した値であり、この人生ゲームの期待値は 50 円になります。
ルーレットの情報とボードの情報を入力とし、ゴール時の所持金の期待値を出力するプログラムを作成してください。
Input
複数のデータセットの並びが入力として与えられます。入力の終わりはゼロみっつの行で示されます。各データセットは以下の形式で与えられます。
X Y Z V1 V2 ... VX N1 E1 A1 N2 E2 A2 : NZ EZ AZ
X (1 ≤ X ≤ 4)、Vi (1 ≤ Vi ≤ 10)、Y (1 ≤ Y ≤ 50)、Ni (1 ≤ Ni ≤ Y-1)、Z (0 ≤ Z ≤ Y-1)、Ei (1 ≤ Ei ≤ 3)、 Ai (1 ≤ Ai ≤ 100) は整数で与えられます。
データセットの数は 100 を超えません。
Output
入力データセットごとに、最終的な所持金の期待値を1行に出力します。なお、所持金の期待値は小数点以下切り捨ての整数で出力してください。
Sample Input
1 2 0 1 1 2 1 1 1 2 100 1 2 1 2 1 2 100 2 2 1 1 2 1 2 100 4 5 3 1 2 3 4 1 1 2 2 2 100 4 3 60 0 0 0
Output for the Sample Input
0 100 0 50 20