最後の扉
秘境の地"ナラマンダ地方"
この奥深い洞窟に眠る黄金の伝説を求め、探検家ボブとマイクは様々な困難に立ち向かいました。ようやくたどり着いた最後の扉。この先には夢に見た黄金が待っています。
その扉には多数の三角形が描かれていました。試しにマイクがその 1 つに触れてみると、その三角形は光を放ちました。光は三角形の底辺から垂直に頂点方向へ長方形を描きながら伸びていき、その先にある別の三角形に触れました。すると、光に触れた三角形も同じように光を放ち、それを繰り返していきました。
扉の三角形は全て二等辺三角形(正三角形は含まない)で、どれも同じ大きさで、どれも重ならず(かつ触れることなく)、またどれも光は一定の距離だけ伸びていました。最後の三角形が光り終えると、そこには何事もなかったかのような静けさが戻ってきました。
ボブは自分の足下に奇妙なメッセージを見つけました。
「むやみに触れるべからず。汝正しくこの扉に触れたとき、この扉は放たれん。 」
ボブとマイクはこのメッセージの意味を考えながら、 何度も三角形に触れてみましたがなかなか扉は開きません。 しかし、それを繰り返していくうちに、二人はメッセージの意味がだんだん分かってきました。
「"むやみに触れるべからず"とは、扉に触れる回数は最小ということ。
できるだけ少ない回数で触れて、全ての三角形を光らせれば、きっと扉は開くはずだ!」
例えば、扉には図 1 のように複数の二等辺三角形が描かれています。
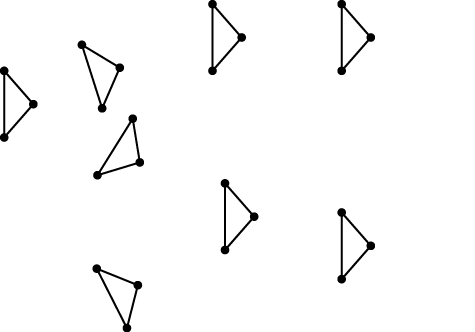
図 1
最初に左下の三角形に触れると、図 2 に示すように、その三角形の底辺から垂直に頂点方向へ光が放たれ、その光が触れる三角形が次々に光ります。
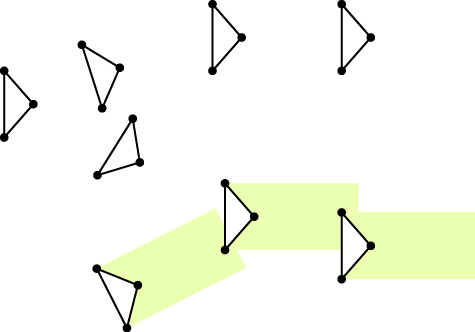
図 2
次に左端の三角形に触れると、図 3 に示すように、全ての三角形が光ります。この手順が全ての三角形を光らせるための最少の手数(2 手)となります。
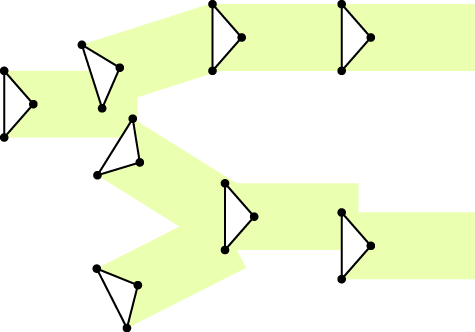
図 3
さあ、ボブとマイクが最後の扉を開ける手助けをしよう。
扉に描かれている三角形の個数、光の伸びる長さ、それぞれの三角形の頂点の座標を入力とし、全ての三角形を光らせるために扉に触れる最少の回数を出力するプログラムを作成して下さい。光の伸びる長さは、底辺からの長さであるものとします。また、光はそれを放つ三角形の頂点を含むような十分な長さを持ちます。
なお、この問題を解くにあたっては、2 点の距離が 0.01 以下の場合には、同一の点と処理します。また、1 点とひとつの直線の距離が 0.01 以下の場合には、この点はこの直線上にあるとして処理します。
Input
複数のデータセットの並びが入力として与えらる。入力の終わりはゼロふたつの行で示される。各データセットは以下の形式で与えらる。
n d T1 T2 : Tn
1行目に扉に描かれている三角形の個数 n (1 ≤ n ≤ 100) と光の伸びる長さを表す整数 d (1 ≤ d ≤ 1000) が与えられる。
続く n 行に各三角形の情報 Ti が以下の形式で与えられる。
x1 y1 x2 y2 x3 y3
三角形の3つの頂点の座標が整数で与えられる(-1000 ≤ x1, y1, x2, y2, x3, y3 ≤ 1000)。
データセットの数は 20 を超えない。
Output
データセットごとに、扉に触れる最少の回数を1行に出力する。
Sample Input
3 4 1 0 3 0 2 1 2 3 2 5 3 4 5 3 5 5 6 4 3 2 1 0 3 0 2 1 2 3 2 5 3 4 5 3 5 5 6 4 0 0
Output for the Sample Input
1 3