四元数のかけ算
複素数を拡張したものに四元数と呼ばれるものがあります。物体の回転などを表現するのに便利なので、ロボットの腕の制御などに使える便利な数です。四元数は、4つの実数 $x$、$y$、$z$、$w$ と特別な数(虚数を拡張したもの)$i$、$j$、$k$ を用いて、$x + yi + zj + wk$ と表されます。このような四元数の和は次のように定義されます。
$(x_1 + y_1 i + z_1 j + w_1 k) + (x_2 + y_2 i + z_2 j + w_2 k) = (x_1 + x_2) + (y_1 + y_2)i + (z_1 + z_2)j + (w_1 + w_2)k$
一方、1、$i$、$j$、$k$ の間の積は次のように与えます。
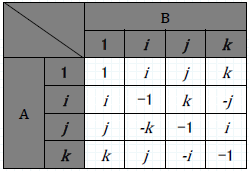
この表は、2つの特別な数 $A$ と $B$ の積 $AB$ を表しています。例えば、 $i$ と $j$ の積 $ij$ は $k$ であり、 $j$ と $i$ の積 $ji$ は $-k$ であることを表しています。
一般の四元数の積は、この関係を満たすように計算されます。例えば、2つの四元数、$1+2i+3j+4k$ と$7+6i+7j+8k$ の積は次のように計算します。
$(1+2i+3j+4k) \times (7+6i+7j+8k)=$
$7+6i+7j+8k$
$+14i+12i^2+14ij+16ik$
$+21j+18ji+21j^2+24jk$
$+28k+24ki+28kj+32k^2$
上の表を適用することにより
$= -58+16i+36j+32k$
となります。
4つの係数$x$、$y$、$z$、$w$ が整数でかつすべてがゼロとはならない2つの四元数 ($x_1+y_1 i+z_1 j+w_1 k$) と($x_2+y_2 i+z_2 j+w_2 k$)を入力とし、その積を($x_3+y_3 i+z_3 j+w_3 k$)とする時の$x_3$、$y_3$、$z_3$、$w_3$ を出力するプログラムを作成してください。
入力
複数のデータセットが与えられます。入力の終わりはゼロひとつの行で示されます。各データセットは以下の形式で与えられます。
$n$
$data_1$
$data_2$
:
$data_n$
1行目に処理を行う四元数の組の個数 $n$ ($ n \leq 10$) が与えられます。続く $n$ 行に $i$ 番目の四元数の組の情報 $data_i$ が次の形式で与えられます。
$x_1$ $y_1$ $z_1$ $w_1$ $x_2$ $y_2$ $z_2$ $w_2$
与えられる係数はすべて-1000 以上1000 以下とします。データセットの数は 50 を超えません。
出力
データセットごとに、与えられた四元数の組の積を出力します。
入力例
2 1 2 3 4 7 6 7 8 5 6 7 8 3 2 3 4 0
出力例
-58 16 36 32 -50 32 28 48