ねこまっしぐら２

あるところに大きな古いお屋敷があり、１匹のねこが住み着いていました。図のように、お屋敷は上空から見ると凸多角形になっており、まっすぐな壁で囲まれたいくつかの部屋で造られています。１枚の壁はその両端にある柱によって支えられています。お屋敷はとても古いため、どの壁にもねこが通ることができるくらいの穴が１つ空いています。ねこは壁の穴を通ってお屋敷の部屋と部屋または部屋と外を行き来することができます。

お屋敷のご主人は、ねこに餌をあげるために、口笛を吹いてねこをお屋敷の外へ呼び出します。ねこはとても賢く、ご主人が口笛を吹くと、「最良の選択」でお屋敷の外へ抜け出します。つまり、最も少ない回数だけ穴を通って外へ出ます。

ねこはとても気まぐれで、どの部屋にいるか分かりません。そのため、ねこがお屋敷の外へ出るのにかかる時間は日によって異なり、ご主人はどれだけ待てばよいかわからず困っていました。ある時ご主人は、ねこが穴を通り抜けるときに、とても時間がかかっていることに気が付きました。ということは、ねこが外に出るのにかかる時間は穴を通る回数によって決まることになります。ご主人は、ねこが「最良の選択」をした場合の穴を通る回数の最大値が分かれば、ねこがどの部屋にいたとしても、最大どれだけ待てばよいか分かるのではないかと考えました。ご主人はお屋敷の間取りを知っていますが、お屋敷はとても大きく、自分では計算することができません...。

お屋敷の間取りを読み込み、ねこが「最良の選択」をした場合、外に出るまでに通る穴の数の最大値を 出力するプログラムを作成して下さい。

入力

入力は複数のデータセットからなる。入力の終わりはゼロ２つの行で示される。各データセットは以下の形式で与えられる。

C W
x1 y1
x2 y2
:
xC yC
s1 t1
s2 t2
:
sW tW

各行で与えられる数値は１つの空白で区切られている。

１行目に柱の数 C (3 ≤ C ≤ 100) と壁の数 W (3 ≤ W ≤ 300) が与えられる。続く C 行に柱の座標が与えられる。x_i (-1000 ≤ x_i ≤ 1000) は i 番目の柱の x 座標、y_i (-1000 ≤ y_i ≤ 1000) は i 番目の柱の y 座標をそれぞれ示す整数である。柱にはそれぞれ 1 から C までの番号が割り当てられている。 続く W 行に壁の情報が与えられる。

s_i (1 ≤ s_i ≤ C)、t_i (1 ≤ t_i ≤ C) は壁の両端を支える柱の番号を示す。

入力は以下の条件を満たすと考えてよい。

• 異なる柱が同じ位置を占めることはない。
• 異なる壁が重なったり、柱以外で交差することはない。
• １つの柱は２つ以上の壁を支えている。
• 壁の長さは 0 より大きい。
• 柱は壁の両端だけにある。つまり、柱が壁の途中にあることはない。
• 壁は異なる２つの部屋、あるいは部屋と外とを仕切る。
• 任意の異なる２つの柱を選んだとき、互いの柱には壁をたどって到達できる。

データセットの数は 50 を超えない。

出力

データセットごとに、ねこが「最良の選択」をした場合、外に出るまでに通る穴の数の最大値を１行に出力する。

入力例

4 4
0 0
1 0
1 1
0 1
1 2
1 4
2 3
3 4
12 22
2 0
4 0
8 0
4 2
6 2
8 2
2 4
4 4
6 4
0 6
8 6
0 8
1 2
2 3
1 4
1 7
1 10
2 4
2 5
3 5
3 6
4 5
4 8
5 6
5 9
6 9
6 11
7 10
7 8
8 9
9 11
10 11
10 12
11 12
0 0

出力例

1
3

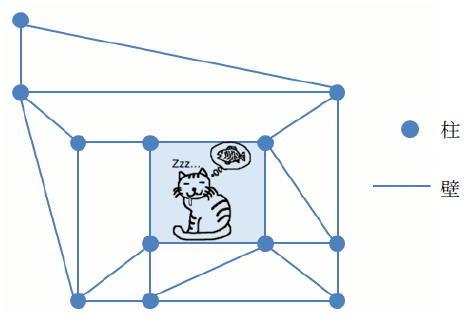
２つ目のデータセットが、冒頭の図に示したお屋敷の間取りに対応する。図のように、薄く色が塗られた部屋にねこがいるときは、「最良の選択」で外に出るまでに通り抜ける穴の数は３つである。それ以外の部屋にねこがいるときは、２つ以下で外に出られる。したがって、ねこが「最良の選択」をしたとき、外に出るまでに通り抜ける穴の数の最大値は 3 になる。

---