古代遺跡の謎

古代遺跡から超大型あみだくじが発見された。学者達はこれをVLA(Very Long Amidakuji)と命名した。分析の結果、VLAは N 本の縦棒を持ついくつかの部品の組み合わせで構成され、多くの場合繰り返しを含んでいることがわかった。例えば、図のVLAは２種類の部品AとBを使った４つの部品から構成されている。

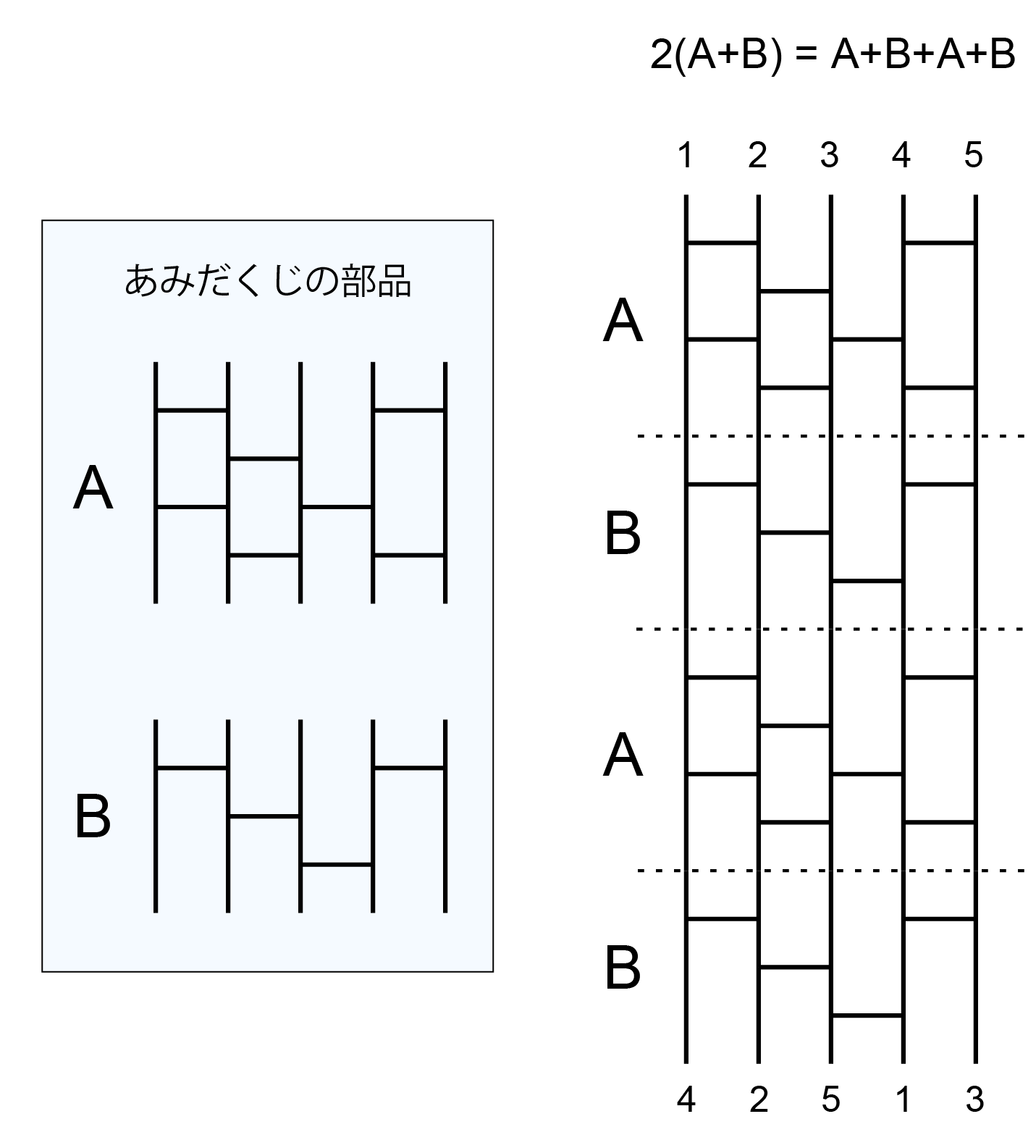
このVLAの上端に左から順番に 1,2,3,4,5 と番号をつけ、それぞれの番号からVLAをたどり（あみだくじのたどり方については問題文最後の補足を参照してください)、下端にたどり着いた場所の縦棒にその番号を振る。すべての番号についてたどり終えた後で、下端に振られた番号を左から読むと 4,2,5,1,3 になる。このように、1,2,3,4,5 という番号の列が 4,2,5,1,3 という列に変換される。

彼らはVLAによって 1 から N までの番号の列がどのように変換されるのかを知りたいが、手作業でたどるのは大変そうだ。そこでパソコン甲子園出場者である優秀なプログラマーの君たちに、VLAのシミュレーションを依頼した。

VLAはとても長いため、そのままの状態ではプログラマーたちに情報を伝えることができない。そこで学者たちは、部品の種類を英大文字１つで表し、VLAを式で表現することにした。

部品は同じ位置関係である縦棒が一致するように、左から順番に + 演算子で接続される。たとえば、上からA,B,C,D という順番で連結された部品の列は A+B+C+D という式で表記される。

部品の列を表す式 seq の m 回の繰り返しは、m(seq) と表記できる。たとえば、A+B の2回の繰り返しは 2(A+B) と表せ、これは A+B+A+B と同じである。また、seq が１つの部品 a の場合は、a を囲むかっこを省略しても構わない。4(A+B) と 3(X+Y) を、この順番で連結したVLAは 4(A+B)+3(X+Y) と表せる。また、かっこは 2(4(A+B)+3(X+Y))+10C のように入れ子にしても構わない。

それでは、縦棒の数 N、各部品の情報、複数のVLAの式を入力とし、各式が表すVLAによって1から N までの番号の列がどのように変換されるかを出力するプログラムを作成しなさい。

（※補足：あみだくじのたどり方について）
あみだくじのある縦棒の上端から出発して上から下へ進む。ただし、横棒がある地点ではその横棒でつながった別の縦棒に移動する。これを、縦棒の下端にたどり着くまで繰り返す。

入力

入力は１つのデータセットからなる。入力データは以下の形式で与えられる。

N K
p1 h1
g1(1,1) g1(1,2) .. g1(1,N-1)
g1(2,1) g1(2,2) .. g1(2,N-1)
:
g1(h1-1,1) g1(h1-1,2) .. g1(h1-1,N-1)
p2 h2
g2(1,1) g2(1,2) .. g2(1,N-1)
g2(2,1) g2(2,2) .. g2(2,N-1)
:
g2(h2-1,1) g2(h2-1,2) .. g2(h2-1,N-1)
:
pK hK
gK(1,1) gK(1,2) .. gK(1,N-1)
gK(2,1) gK(2,2) .. gK(2,N-1)
:
gK(hK-1,1) gK(hK-1,2) .. gK(hK-1,N-1)
E
expression1
expression2
:
expressionE

1行目に縦棒の数を表す整数 N (2 ≤ N ≤ 12) と部品の種類の数 K (1 ≤ K ≤ 26)が与えられる。

2行目以降に K 種類の部品の情報が与えられる。各部品は以下の形式で与えられる。

• 最初の行は部品名を表す１つの英大文字 p_i と部品 i の縦棒の長さを表す整数 h_i (1 ≤ h_i ≤ 20)を含む。
• 続くh_i-1 行で部品 i の横棒の情報が与えられる。g_i(r, c) は部品 i の上端から長さ r の位置において、左から c 番目の縦棒と c+1 番目の縦棒をつなぐ横棒の有無を表す。横棒があるときは g_i(r, c) = 1、横棒がないときは g_i(r, c) = 0である。

続く１行に式の数 E (1 ≤ E ≤ 100) が与えられる。続く E 行にVLAの式を表す文字列 expression_i（1文字以上1000文字以下）が与えられる。

入力は以下の条件を満たす。

• 異なる部品に同じ名前が使われることはない。
• 各部品 i について、g_i(r, c)と g_i(r, c+1)が同時に 1 となることはない。
• 式に含まれる整数は 1 以上 1,000,000,000 以下である。
• 式には空白は含まれない。

出力

式ごとに、VLAによる1からNまでの列の変換結果を１行に出力する。それぞれの数字の間は空白1つで区切る。

入出力例

入力例

5 2
A 5
1 0 0 1
0 1 0 0
1 0 1 0
0 1 0 1
B 4
1 0 0 1
0 1 0 0
0 0 1 0
2
2(A+B)
1000000000(1000000000A+1000000000B)

出力例

4 2 5 1 3
1 2 3 4 5

---