力持ち
力持ちたちが集う力持ち学園がありました。力持ち学園の運動会では、力持ちたちが隊列を組んで行進します。
力持ちたちは常に自分たちの力を誇示したい一方で、彼らの大半は自分で歩きたくありません。そこで彼らの一部が一番下になり、その上に大勢の人を縦一列に持ちあげて歩くことで、実際に歩く人数を減らそうと考えました。
はじめに、N 人の力持ちは地面の上に横一列に並んでいて、それぞれ左側から 1,2,3,..., N と通し番号で呼ばれています。通し番号 i の力持ちの体重は wi で最大 ci の重量まで持つことができます。
力持ちは、以下の条件をすべて満たすときだけ、隣に立っている左右どちらかの力持ちを持ちあげることができます。
- 自分の上下には力持ちはいない。つまり、誰かに持ち上げられてもいないし、誰かを持ちあげてもいない。
- 隣の力持ちの体重が、自分が持つことのできる最大の重量以下である。ただし、隣の力持ちが既に誰かを持ち上げているなら、縦に積み上がった力持ちたちの体重の合計が、自分が持つことのできる最大の重量以下でなければならない。
例えば、次のような3人の力持ちの隊列を考えてみましょう。
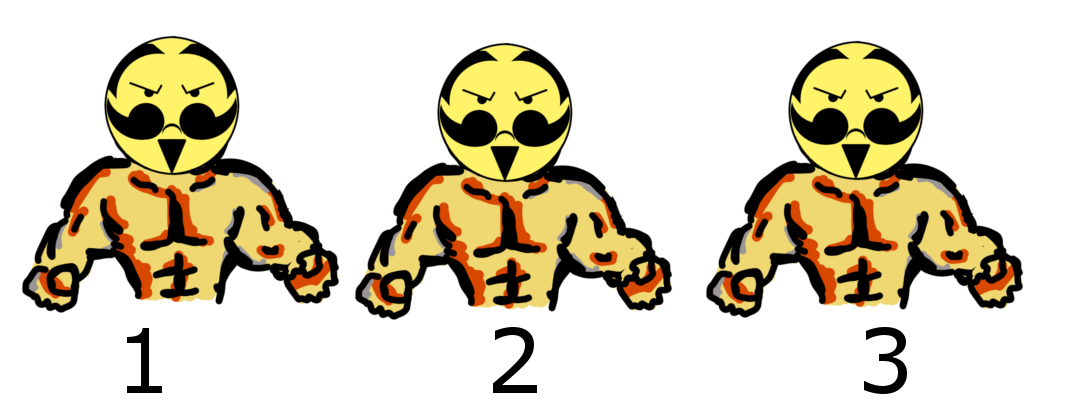
下図のように、2の力持ちが持つことのできる重さが w3 以上のとき、2の力持ちは3の力持ちを持ちあげることができます。続いて、1の力持ちが持つことのできる重さが w2 + w3 以上のとき、1の力持ちは2の力持ちを持ちあげることができます。
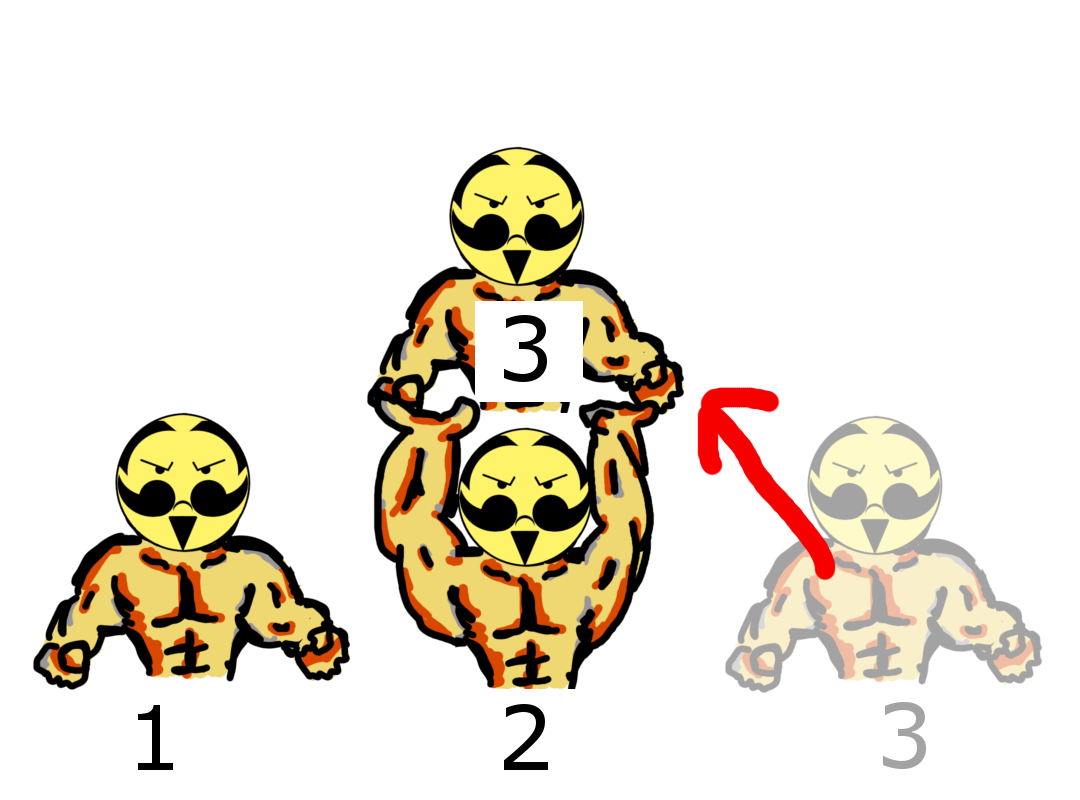 |
→ | 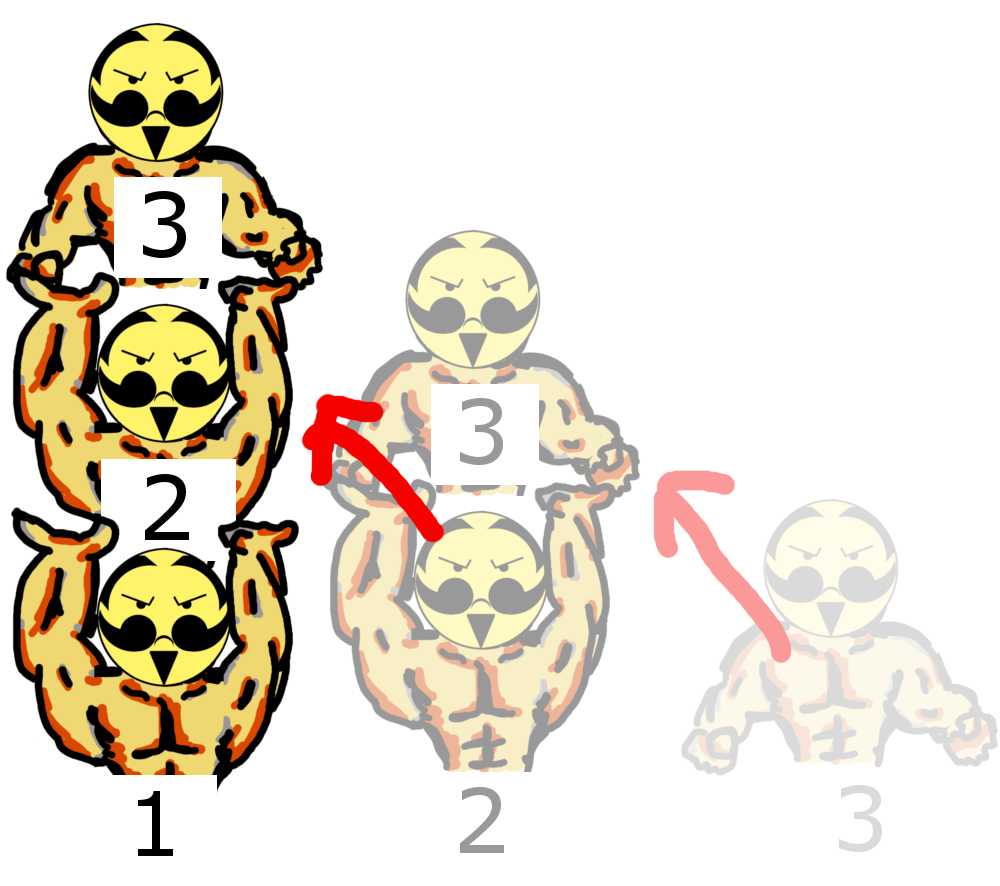 |
また、下図のように3の力持ちが2の力持ちを持ちあげた場合は、1の力持ちの隣が、2の力持ちを持った3の力持ちになるので、1の力持ちは3の力持ちを持ちあげることができます。
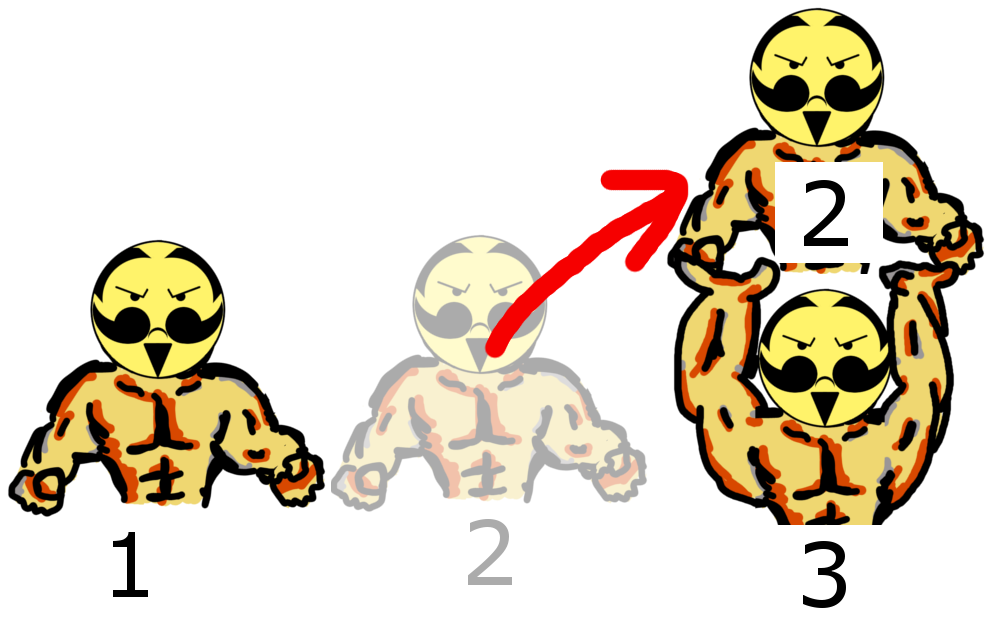 |
→ | 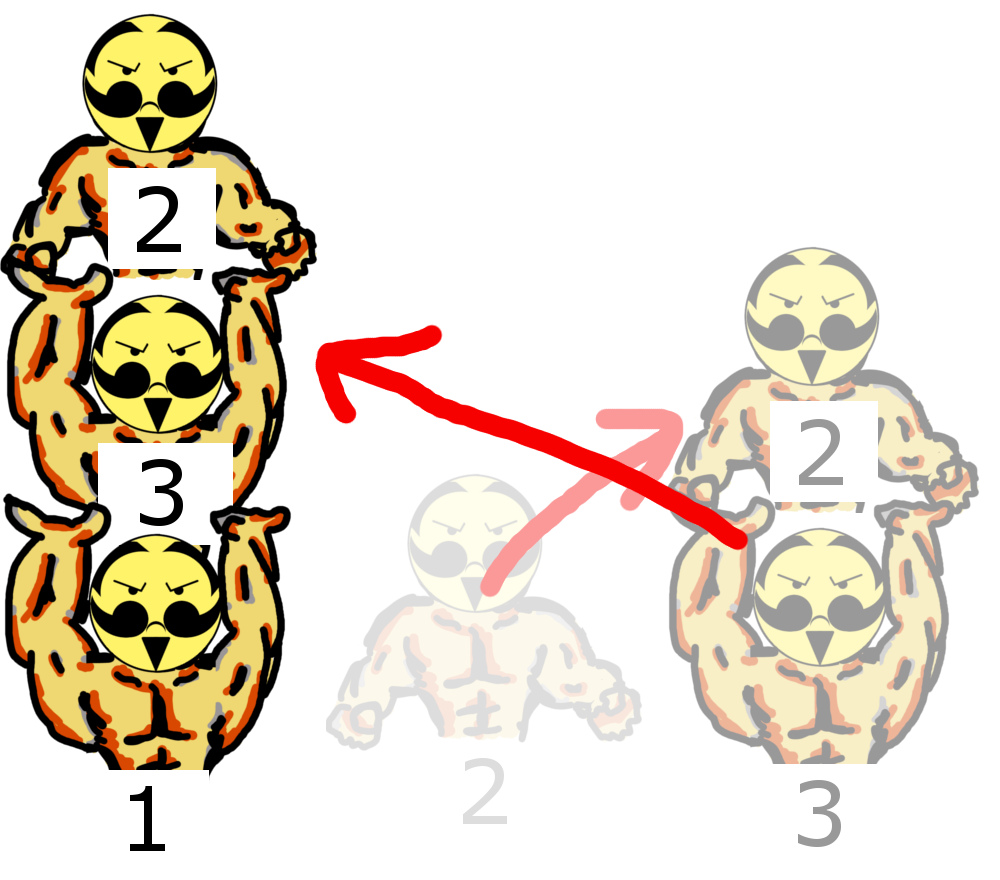 |
2の力持ちが、下の図のように1と3の力持ちを両方持つことはできません。

力持ち学園の専属プログラマーとして、一番下で歩くことになる最小の人数を求めてください。
入力
入力は以下の形式で与えられる。
N c1 w1 c2 w2 : cN wN
1 行目に力持ちの人数 N (1 ≤ N ≤ 1000) が与えられる。続く N 行に i 番目の力持ちが持てる重量の最大値 ci (1 ≤ ci ≤ 100000) と体重 wi (1 ≤ wi ≤ 100000) が与えられる。
出力
最小の人数を1行に出力する。
入出力例
入力例1
3 150 120 100 50 80 100
出力例1
1
入力例2
8 50 100 20 20 30 20 90 50 140 30 30 60 59 120 10 10
出力例2
3