Disc

　

A mysterious device was discovered in an ancient ruin. The device consists of a disc with integers inscribed on both sides, a bundle of cards with an integer written on each of them and a pedestal within which the cards are placed. The disc rotates when the bundle of cards is put into the pedestal. Only one side of the disc is exposed to view at any one time.

The disc is radially segmented in equal angles into $K$ sections, and an integer, from $1$ to $K$ in increasing order, is inscribed clockwise on each section on the front side. The sections on the back side share the same boundaries with the front side, and a negative counterpart of that in the section on the front side is inscribed, i.e., if $X$ is inscribed in the front side section, $-X$ is inscribed on the counterpart section on the back side. There is a needle on the periphery of the disc, and it always points to the middle point of the arc that belongs to a section. Hereafter, we say "the disc is set to $X$" if the front side section just below the needle contains an integer $X$.

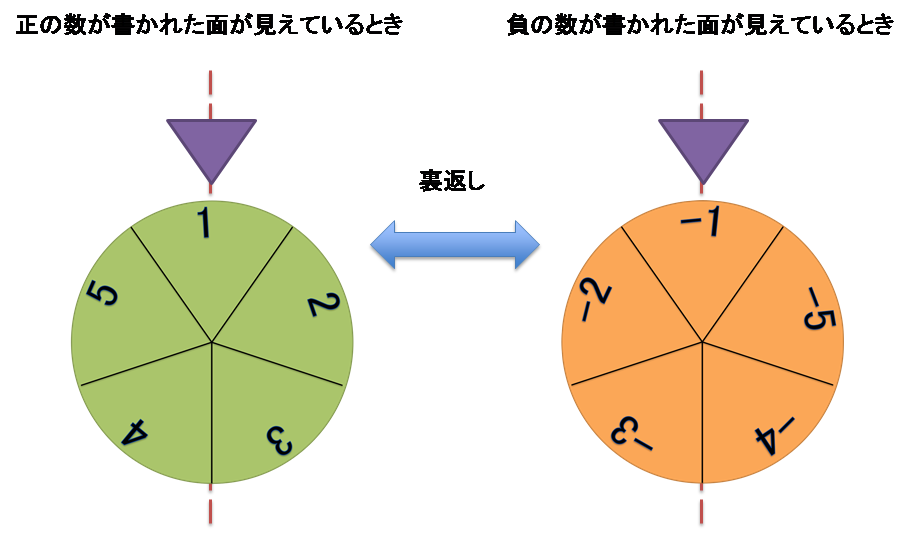
Fig.1 Disc with 5 sections (i.e., $K = 5$): When the disc is set to $1$ on the front side, it is set to $-1$ on the back side.

Investigation of the behavior of the device revealed the following:

When the bundle of cards is placed in the pedestal, the device sets the disc to 1.
Then, the device reads the cards slice by slice from top downward and performs one of the following actions according to the integer $A$ on the card

• If $A$ is a positive number, it rotates the disc clockwise by $|A|$ sections.
• If $A$ is zero, it turns the disc back around the vertical line defined by the needle and the center of the disc.
• If $A$ is a negative number, it rotates the disc counterclockwise by $|A|$ sections.

It is provided that $|A|$ is the absolute value of $A$. The final state of the device (i.e., to what section the needle is pointing) varies depending on the initial stacking sequence of the cards. To further investigate the behavior of the device, we swapped two arbitrary cards in the stack and placed the bundle in the pedestal to check what number the disc is set to. We performed this procedure over again and again.

Given the information on the device and several commands to swap two cards, make a program to determine the number to which the device is set at the completion of all actions. Note that the stacking sequence of the cards continues to change as a new trial is made.

Input

The input is given in the following format.

$K$ $N$ $Q$
$A_1$ $A_2$ ... $A_N$
$L_1$ $R_1$
$L_2$ $R_2$
$...$
$L_Q$ $R_Q$

The first line provides the number of sections $K$ ($2 \leq K \leq 10^9$), the slices of cards $N$ ($2 \leq N \leq 100,000$), and the number of commands $Q$ ($1 \leq Q \leq 100,000$). The second line provides an array of $N$ integers inscribed on the sections of the disc. $A_i$ ($-10^9 \leq A_i \leq 10^9$) represents the number written on the $i$-th card from the top. Each of the subsequent $Q$ lines defines the $i$-th command $L_i,R_i$ ($1 \leq L_ i < R_i \leq N$) indicating a swapping of $L_i$-th and $R_i$-th cards from the top followed by placing the card bundle in the device.

Output

For each command, output a line containing the number to which the device is set at the completion of all actions.  

Sample Input 1

5 3 1
1 -2 0
2 3

Sample Output 1

-3

The device moves as follows while it is performing the first command.

1 0 -2

When the first command is performed, the stacking sequence of the card bundle, from top to bottom, changes to the sequence shown below.

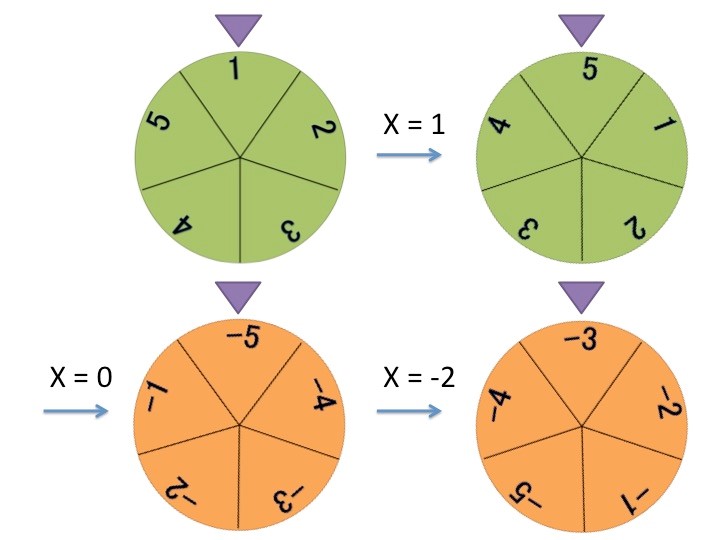
Fig.2 An illustrative example of how the device works

Therefore, the device is set to -3 after all actions have completed. Output this value.

Sample Input 2

5 7 5
0 0 3 3 3 3 3
1 2
2 3
3 4
4 5
5 6

Sample Output 2

1
2
3
4
5

---