ぴょんぴょん川渡り
問題
ある川で,一方の岸から石の上を次々と飛び移って反対側の岸まで行くという少々危険なゲームがはやっている.
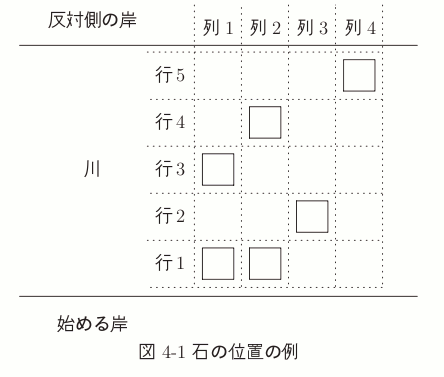
今,図 4-1 のように,石はマス目の上に存在すると考える.行の数は n である. 図 4-1 では n = 5 である.
このゲームでは,一方の岸から始めて,通常のジャンプまたは m 回以下の一行飛ばしのジャンプをして反対側の岸まで渡る.通常のジャンプとは,今いる行の一つ先の行の岸または石のどれかに飛び移ることであり,一行飛ばしのジャンプとは,今いる行の二つ先の行の岸または石のどれかに飛び移ることである.始める岸の一つ先の行は 1 行目,二つ先の行は 2 行目であり,n − 1 行目の二つ先の行,及び n 行目の一つ先の行は反対側の岸であるとする.
さて,このゲームをできるだけ安全に成し遂げるために,ジャンプの危険度というものを考えることにした.それぞれの石には,滑りやすさが定まっている.石から石へ飛び移る際のジャンプの危険度は,通常のジャンプであっても,一行飛ばしのジャンプであっても,
(今いる石の滑りやすさ + 飛び移る先の石の滑りやすさ)×(横の移動距離)
で定める.ただし,横の移動距離とは,列の番号の差である.また,岸から石へ,あるいは石から岸へ飛び移るジャンプの危険度は 0 とする.
入力として n, m,それぞれの石の位置と滑りやすさが与えられたとき,反対側の岸まで到達する際のジャンプの危険度の合計の最小値を求めるプログラムを作成せよ.与えられる入力データは必ず反対側の岸まで到達することができるようになっており,同じマス目に石は 2 個以上存在しない.
入力
入力は複数のデータセットからなる.各データセットは以下の形式で与えられる.
入力の 1 行目には,空白を区切りとして 2 個の整数 n,m が書かれている.これは,行の数と,一行飛ばしのジャンプの許される回数を表す.n,m はそれぞれ 2 ≤ n ≤ 150, 0 ≤ m ≤ (n+1)/2 を満たす.
続く n 行には,それぞれの行にある石の情報が書かれている.i+1 行目 (1 ≤ i ≤ n)には,1 つの整数 ki (0 ≤ ki ≤ 10) と,それに続き 2 × ki 個の整数が空白で区切られ書かれている.これらは,始める岸から数えて i 番目の行にある石の情報を表す.
ki はその行に存在する石の個数を表し,それに続く 2 × ki 個の整数については,2 × j - 1 個目 (1 ≤ j ≤ ki ) の整数 xi,j はその行の j 個目の石の列の番号を,2 × j個目の整数 di,j はその行の j 個目の石の滑りやすさをそれぞれ表す.xi,j ,di,j はそれぞれ 1 ≤ xi,j, di,j ≤1000 を満たす.
採点用データのうち, 配点の 20% 分については, n ≤ 6 を満たし,配点の別の 20%分については, m = 0 を満たす.
n, m がともに 0 のとき入力の終了を示す. データセットの数は 10 を超えない.
出力
データセットごとに, 反対側の岸まで到達する際のジャンプの危険度の合計の最小値を表す 1 つの整数を1 行に出力する.
例
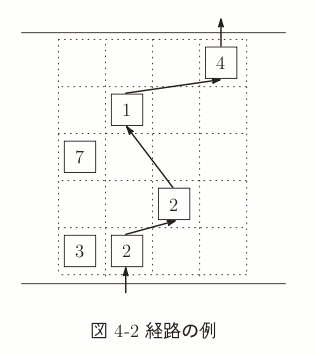
図 4-2 において,石に書かれた数字はそれぞれの石の滑りやすさを表すとする. 矢印で示された順番で石を渡るとき,それぞれのジャンプの危険度は,順番に 0, (2 + 2) × 1 = 4,(2 + 1) × 1 = 3,(1 + 4) × 2 = 10,0 であり,合計は 17 となる. このとき,ジャンプの危険度の合計は最小となる. この例は1つ目の入出力例に対応している.
入出力例
入力例
5 1 2 1 3 2 2 1 3 2 1 1 7 1 2 1 1 4 4 5 0 2 1 3 2 2 1 3 2 1 1 7 1 2 1 1 4 4 0 0
出力例
17 40
上記問題文と自動審判に使われるデータは、情報オリンピック日本委員会が作成し公開している問題文と採点用テストデータです。