あみだくじ

問題

あなたは J 君と一緒にあみだくじを使って遊んでいる.あみだくじは n 本の縦棒と m 本の横棒からなる.縦棒には左から順に 1 から n の番号がついており,縦棒 i の下端には正整数 s_i が書かれている.

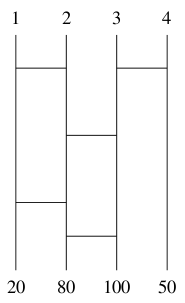
図 3-1 あみだくじの例(n = 4, m = 5, s₁ = 20, s₂ = 80, s₃ = 100, s₄ = 50)

縦棒 i の一番上から順に道をたどっていき到達した下端に書かれている整数が, 縦 棒 i を選んだ場合の得点である.例えば,図 3-1 では,縦棒 1 を選ぶと得点は 80 点 であり,縦棒 2 を選ぶと得点は 100 点である.

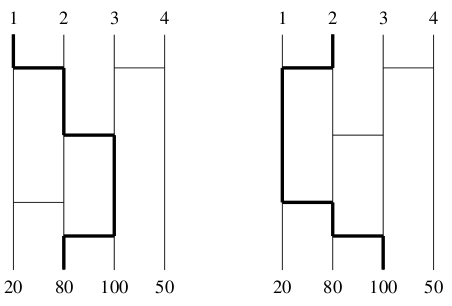
図 3-2 道のたどり方の例

J 君は縦棒 1 から縦棒 k までの連続した k 本を選ぶことにした.それら k 本の縦棒を選んだときの点数の合計が J 君の得点となる.ただし,あなたはあみだくじ内の 横棒を一本選び,その横棒をあみだくじから削除することができる. (削除しなくてもよい.) もし,あなたが横棒を一本削除した場合は,削除後のあみだくじにおいて, 縦棒 1 から縦棒 k までの連続した k 本の縦棒を選んだときの点数の合計が J 君の得点となる.

入力としてあみだくじの形と J 君の選ぶ縦棒の本数 k が与えられたとき,J 君の得 点の最小値を求めるプログラムを作成せよ.

入力

入力は複数のデータセットからなる．各データセットは以下の形式で与えられる．

1 行目には 4 つの整数 n, m, h, k が空白区切りで書かれている. n (2 ≤ n ≤ 1000) は縦棒の本数を, m (1 ≤ m ≤ 100000) は横棒の本数を, h (2 ≤ h ≤ 1000) は縦棒の長さを,k (1 ≤ k ≤ n) は J 君が選ぶ縦棒の本数を表す.

続く n 行には縦棒の下端に書かれている点数が書かれている. i + 1 行目 (1 ≤ i ≤ n)には正整数 s_i が書かれている. また, s₁ + s₂ + ... + s_n ≤ 2000000000 = 2 × 10⁹ を満たす.

続く m 行には横棒の位置が書かれている.横棒には 1 から m までの番号がついている.i + n + 1 行目 (1 ≤ i ≤ m) には, 横棒 i の位置を表す 2 つの整数 a_i, b_i (1 ≤ a_i ≤ n - 1, 1 ≤ b_i ≤ h - 1) が空白区切りで書かれており,横棒 i が縦棒 a_i と縦棒 a_i + 1 を結び, 横棒 i の上端からの距離が b_i であることを表す. ただし,どの 2 つの横棒も端点を共有することはない.

採点用データのうち,配点の 20 % 分は横棒を削除しない場合に J 君の得点が最少となる.また,配点の 30 % 分は n ≤ 20, m ≤ 30, h ≤ 10 を満たし,配点の 60 % 分は m ≤ 1000 を満たす.

入力の終わりは 4つのゼロを含む行で示される. データセットの数は 10 を超えない．

出力

データセットごとに, J 君の得点の最小値を1 行に出力する.

入出力例

入力例

4 5 7 2
20
80
100
50
1 1
2 6
2 3
1 5
3 1
2 2 5 1
10
20
1 1
1 3
0 0 0 0

出力例

100
10

1つ目の例 は図 3-1 に対応し,あなたが横棒 4 (縦棒 1 と縦棒 2 を上端から距離 5 の場所で結ぶ横棒)を削除したとき,J 君の得点は最小になる.例 2 では,あなたが横棒を削除しない場合に J 君の得点が最小になる. (図3-3 を見よ.)

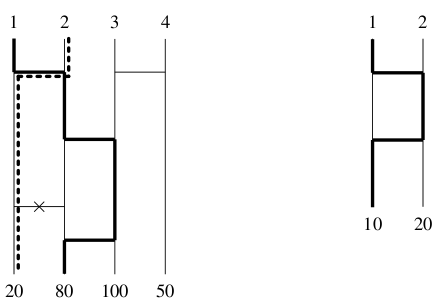
図 3-3

---