お菓子の分割
問題
長さ N ミリメートルの棒状のお菓子が 1 本ある(ここで N は偶数). 2 人の JOI 関係者が,このお菓子を複数本に切断して,合計 N/2 ミリメートルずつに分けること にした.
理由は不明であるが,このお菓子は場所によって切断のしやすさが異なっている. 2 人は,お菓子を左から 1 ミリメートルごとに調べ,各場所で切断に何秒かかるか を割り出した.2 人がお菓子を分けるための切断にかかる秒数の最小値を求めるプ ログラムを作成せよ.
入力
入力の 1 行目には,棒の長さ N(2 ≤ N ≤ 10000 ,ただし N は偶数) が書かれてい る.入力の i + 1 行目 (1 ≤ i ≤ N − 1) には,左端から i ミリメートル目の場所の切 断にかかる秒数を表す整数 ti (1 ≤ ti ≤ 10000) が書かれている.切断可能な場所が N − 1 箇所であることに注意せよ.
採点用データのうち,配点の 5% 分については,高々 2 カ所を切断することで最 小値を実現でき,10% 分については,高々 3 カ所を切断することで最小値を実現で きる.配点の 20% 分については,N ≤ 20 である.
出力
出力は2 人がお菓子を分るための切断にかかる秒数の最小値を含む 1 行からなる.
入出力例
入力例 1
6 1 8 12 6 2
出力例 1
7
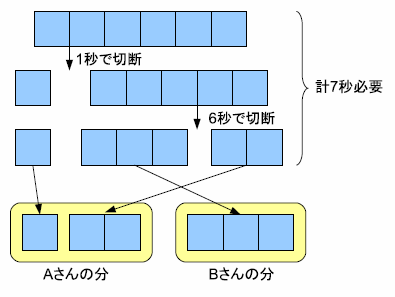
この場合,左端から 1 ミリメートルと 4 ミリメートルの場所で切断するとかかる 秒数が最小となる.かかる秒数は 1 秒と 6 秒で,合計 7 秒である.
上記問題文と自動審判に使われるデータは、情報オリンピック日本委員会が作成し公開している問題文と採点用テストデータです。