たのしいカードゲーム(Card Game is Fun)

1 から1000 までのどれかの整数が書かれたカードがたくさんある．アンナとブルーノはそれらのカードを用いて，次のようなゲームをする．

アンナはA 枚，ブルーノはB 枚のカードからなる山を持つ．アンナはA 枚のカードの中から任意の何枚か（0 枚でもよい）を捨てて新しい山を作る．ブルーノはB, 枚のカードからなる山の一番上から何枚か（0枚でもよい）と，一番下から何枚か（0 枚でもよい）を捨てて新しい山を作る．ただし，捨てる際に残ったカードの並び替えは行わない．このように作った2 つの山が一致していたら，一方の山に含まれるカードの枚数が2 人の得点になる．ただし，2 つの山が一致するとは，山に含まれるカードの枚数n が同じで，かつ上からi 番目(1 ≤ i ≤ n) に書かれたカードの整数が全て同じであることである．

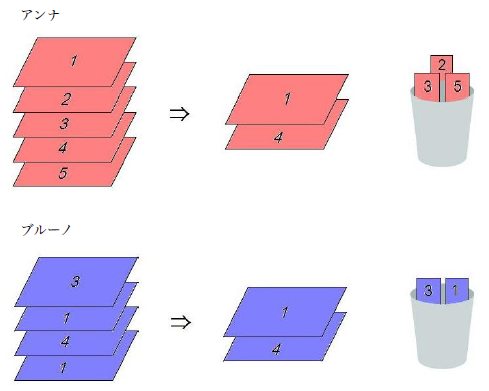
例えば，アンナが5 枚のカードの山を持ち，書かれている整数は上から順に1,2,3,4,5 であり，ブルーノが4 枚のカードの山を持ち，書かれている整数が上から順に3,1,4,1 であったとする．このとき，アンナが2,3,5 のカードを捨て，ブルーノが一番上の3 と一番下の1 のカードを捨てると2 人の山が一致する．このとき，残った山の一方に含まれるカードの枚数は2 枚なので，2 人は得点2 を得る．

2 人の得点の最大値を求めたい．

課題

アンナとブルーノが持っているカードの山の情報が与えられたときに，2 人の得点の最大値を求めるプ ログラムを作成せよ．

制限

1 ≤ A ≤ 5000
1 ≤ B ≤ 5000
カードに書かれている整数は1 以上1000 以下である．

入力

標準入力から以下のデータを読み込め．

1 行目には，整数A, B が空白を区切りとして書かれている．

2 行目には，A 個の整数が空白を区切りとして書かれており，i 番目の整数(1 ≤ i ≤ A) はアンナの持っている山の上からi 番目のカードに書かれている整数を表す．

3 行目には，B 個の整数が空白を区切りとして書かれており，j 番目の整数(1 ≤ j ≤ B) はブルーノの持っている山の上からj 番目のカードに書かれている整数を表す．

出力

標準出力に，得点の最大値を表す整数を1 行で出力せよ．

採点基準

採点用データのうち，配点の10%分については，A ≤ 10, B ≤ 10 を満たす．
採点用データのうち，配点の50%分については，A ≤ 100, B ≤ 100 を満たす．

入出力例

入力例 1

5 4
1 2 3 4 5
3 1 4 1

出力例 1

2

この入出力例は問題文中の例に対応している．

入力例 2

6 5
4 1 5 2 3 4
4 5 4 2 3

出力例 2

3

この入出力例では，2 人が得点3 を得る方法が2 通り存在する．アンナが1, 2, 3 のカードを捨てブルーノが2, 3 のカードを捨てたとき, 2 人の山は上から順に4, 5, 4 となり, 2 人の得点は3 点となる. また, アンナが1, 5, 4 のカードを捨てブルーノが一番上の4 と5 のカードを捨てたとき, 2 人の山は上から順に4, 2, 3となり, 2 人の得点は3 点となる.

---