魚の生息範囲 (Fish)

問題

オーストラリア大陸の西には，広いインド洋が広がっている．海洋研究者である JOI 氏は，インド洋に生息しているある N 種類の魚の性質について研究している．

それぞれの魚の種類に対して，海の中に直方体状の生息範囲が定まっている．魚は境界も含めて生息範囲の中のどの場所にも移動できるが，生息範囲の外に出ることは決してない．海の中の点は，3 つの実数 (x, y, d) によって表される： (x, y, d) は，上空から見たときにある地点を基準にして東に x，北に y 進んだ位置であり，海面からの深さが d の点を表す．ただし，海面は平面であるとする．

JOI 氏は，K 種類以上の魚の生息範囲が重なる場所がどのくらいあるかを知りたい．そのような場所全体の体積を求めるプログラムを作成せよ．

入力

入力は 1 + N 行からなる．

1 行目には，2 つの整数 N, K (1 ≦ K ≦ N ≦ 50) が空白を区切りとして書かれている．これは，魚が N 種類であり，K 種類以上の魚の生息範囲が重なる場所の体積を求めたいことを表す．

続く N 行のうちの i 行目 (1 ≦ i ≦ N) には，6 つの整数 X_i,1, Y_i,1, D_i,1, X_i,2, Y_i,2, D_i,2 (0 ≦ X_i,1 ＜ X_i,2 ≦ 1000000 (= 10⁶)，0 ≦ Y_i,1 ＜ Y_i,2 ≦ 1000000 (= 10⁶)，0 ≦ D_i,1 ＜ D_i,2 ≦ 1000000 (= 10⁶)) が書かれている．これは，i 種類目の魚の生息範囲が 8 点 (X_i,1, Y_i,1, D_i,1), (X_i,2, Y_i,1, D_i,1), (X_i,2, Y_i,2, D_i,1), (X_i,1, Y_i,2, D_i,1), (X_i,1, Y_i,1, D_i,2), (X_i,2, Y_i,1, D_i,2), (X_i,2, Y_i,2, D_i,2), (X_i,1, Y_i,2, D_i,2) を頂点とする直方体であることを表す．

出力

K 種類以上の魚の生息範囲が重なる場所全体の体積を 1 行で出力せよ．

入出力例

入力例 1

3 2
30 50 0 50 70 100
10 20 20 70 90 60
40 60 20 90 90 70

出力例 1

49000

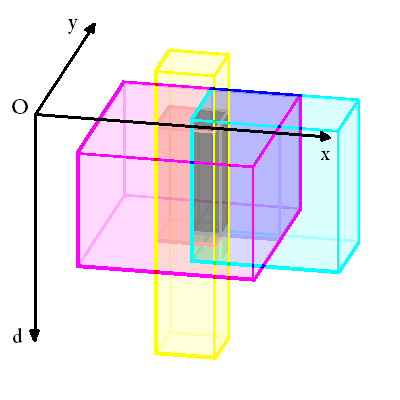
入出力例 1 において，例えば，点 (45, 65, 65) は 1 種類目の魚と 3 種類目の魚の生息範囲であるので，条件を満たす場所である．一方，点 (25, 35, 45) は 2 種類目の魚のみの生息範囲であるので，条件を満たす場所ではない．また，魚の生息範囲は下の図のようになっている．点 O は海面上の基準の地点を表す．

入力例 2

1 1
0 0 0 1000000 1000000 1000000

出力例 2

1000000000000000000

---