問題 3: 超都観光 (Super Metropolis)

問題

JOI 君は，IOI 国にある超都という都市の観光ツアーを計画することになった．

超都は，南北方向にまっすぐに伸びる W 本の道路と，東西方向にまっすぐに伸びる H 本の道路により，碁盤の目の形に区分けされている．

南北方向の W 本の道路には，西から順に 1, 2, ... , W の番号が付けられている．また，東西方向の H 本の道路には，南から順に 1, 2, ... , H の番号が付けられている．西から i 番目の南北方向の道路と，南から j 番目の東西方向の道路との交差点を (i, j) で表す．

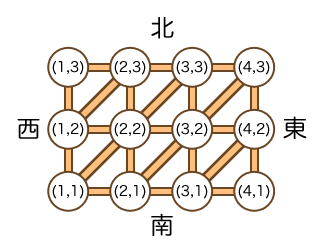
さらに，下図のように，各交差点からは１つ北東の交差点への道がある（最も北の道路上の交差点と最も東の道路上の交差点を除く）． また，１つ南西の交差点への道もある（最も南の道路上の交差点と最も西の道路上の交差点を除く）． すなわち，交差点 (i, j) からは，もし交差点 (i - 1, j), (i + 1, j), (i, j - 1), (i, j + 1) があるときは，それらの交差点へ１本の道を使って行くことが出来る．それに加え，もし交差点 (i - 1, j - 1), (i + 1, j + 1) があるときは，それらの交差点へも１本の道を使って行くことが出来る．

JOI 君はツアーの計画として既に N 個の観光スポットをどのような順番で訪れるかを決めている． i 番目 (1 ≦ i ≦ N) に訪れる観光スポットは交差点 (X_i, Y_i) にある． JOI 君は，ツアーにかかる時間をできるだけ短くするために，通らなければならない道の本数を少なくしたい． 観光スポットを事前に決めた順番で訪れるために通らなければならない道の本数の合計の最小値を求めるプログラムを作成せよ．

ただし，ツアーの開始地点は交差点 (X₁, Y₁) である．また，ツアーの途中で超都の外へ移動してはならないものとする． また，JOI 君は，観光スポットのある交差点を，観光スポットを訪れずに通過することもできる．

「道の本数の合計」についての補足．ツアーの途中で同じ道を２回以上通ることもできる．その場合，「道の本数の合計」としては，その道については通った回数だけ重複して数えるものとする．

入力

入力は 1 + N 行からなる．

1 行目には，空白を区切りとして 3 つの整数 W, H, N (2 ≤ W ≤ 10000, 2 ≤ H ≤ 10000, 1 ≤ N ≤ 1000) が書かれている．

続く N 行のうちの i 行目 (1 ≤ i ≤ N) には，2 つの整数 X_i, Y_i (1 ≤ X_i ≤ W, 1 ≤ Y_i ≤ H) が空白を区切りとして書かれている．これは，i 番目に訪れる観光スポットのある交差点が (X_i, Y_i) であることを表す．

出力

観光スポットを順番に訪れるために通る道の本数の合計の最小値を 1 行で出力せよ．

入出力例

入力例 1

4 3 3
1 1
3 3
4 1

出力例 1

5

入出力例 1 では，例えば (1, 1), (2, 2), (3, 3), (3, 2), (4, 2), (4, 1) の順で交差点を訪れれば良い．

入力例 2

4 3 5
1 3
4 3
2 2
2 2
1 3

出力例 2

7

入出力例 2 のように，同じ交差点に複数回訪れることもある．

---