Kingdom of JOIOI

The Kingdom of JOIOI is a rectangular grid of $H \times W$ cells. In the Kingdom of JOIOI, in order to improve efficiency of administrative institutions, the country will be divided into two regions called "JOI" and "IOI."

Since we do not want to divide it in a complicated way, the division must satisfy the following conditions:

• Each region must contain at least one cell.
• Each cell must belong to exactly one of two regions.
• For every pair of cells in the JOI region, we can travel from one to the other by passing through cells belonging to the JOI region only. When move from a cell to another cell, the two cells must share an edge. The same is true for the IOI region.
• For each row or column, if we take all the cells in that row or column, the cells belonging to each region must be connected. All the cells in a row or column may belong to the same region.

Each cell has an integer called the altitude. After we divide the country into two regions, it is expected that traveling in each region will be active. But, if the difference of the altitudes of cells are large, traveling between them becomes hard. Therefore, we would like to minimize the maximum of the difference of the altitudes between cells belonging to the same region. In other words, we would like to minimize the larger value of

• the difference between the maximum and the minimum altitudes in the JOI region, and
• the difference between the maximum and the minimum altitudes in the IOI region.

Task

Given the altitudes of cells in the Kingdom of JOIOI, write a program which calculates the minimum of the larger value of the difference between the maximum and the minimum altitudes in the JOI region and the difference between the maximum and the minimum altitudes in the IOI region when we divide the country into two regions.

Input

Read the following data from the standard input.

• The first line of input contains two space separated integers $H$, $W$. This means the Kingdom of JOIOI is a rectangular grid of $H \times W$ cells.
• The $i$-th line ($1 \leq i \leq H$) of the following $H$ lines contains $W$ space separated integers $A_{i,1}, A_{i,2}, ..., A_{i,W}$. This means the cell in the $i$-th row from above and $j$-th column from left ($1 \leq j \leq W$) has altitude $A_{i,j}$.

Output

Write one line to the standard output. The output contains the minimum of the larger value of the difference between the maximum and the minimum altitudes in the JOI region and the difference between the maximum and the minimum altitudes in the IOI region when we divide the country into two regions.

Constraints

All input data satisfy the following conditions.

• $2 \leq H \leq 2 000．$
• $2 \leq W \leq 2 000．$
• $1 \leq A_{i, j} \leq 1 000 000 000 (1 \leq i \leq H, 1 \leq j \leq W)．$

Sample Input and Output

Sample Input 1

4 4
1 12 6 11
11 10 2 14
10 1 9 20
4 17 19 10

Sample Output 1

11

For example, in this sample input, we divide the country into two regions as follows. Here, ‘J’ denotes the JOI region, and ‘I’ denotes the IOI region.

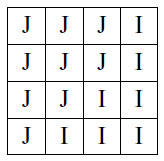
The following division does not satisfy the condition because, in the third column from left, cells with ‘I’ are not connected.

Sample Input 2

8 6
23 23 10 11 16 21
15 26 19 28 19 20
25 26 28 16 15 11
11 8 19 11 15 24
14 19 15 14 24 11
10 8 11 7 6 14
23 5 19 23 17 17
18 11 21 14 20 16

Sample Output 2

18

---