Soccer
You are a manager of a prestigious soccer team in the JOI league.
The team has $N$ players numbered from 1 to $N$. The players are practicing hard in order to win the tournament game. The field is a rectangle whose height is $H$ meters and width is $W$ meters. The vertical line of the field is in the north-south direction, and the horizontal line of the field is in the east-west direction. A point in the field is denoted by ($i, j$) if it is $i$-meters to the south and $j$ meters to the east from the northwest corner of the field.
After the practice finishes, players must clear the ball. In the beginning of the clearance, the player $i$ ($1 \leq i \leq N$) stands at ($S_i, T_i$). There is only one ball in the field, and the player 1 has it. You stand at ($S_N, T_N$) with the player $N$. The clearance is finished if the ball is passed to ($S_N, T_N$), and you catch it. You cannot move during the clearance process.
You can ask players to act. But, if a player acts, his fatigue degree will be increased according to the action. Here is a list of possible actions of the players. If a player has the ball, he can act (i),(ii), or (iii). Otherwise, he can act (ii) or (iv).
- (i) Choose one of the 4 directions (east/west/south/north), and choose a positive integer $p$. Kick the ball to that direction. Then, the ball moves exactly p meters. The kicker does not move by this action, and he loses the ball. His fatigue degree is increased by $A \times p + B$.
- (ii) Choose one of the 4 directions (east/west/south/north), and move 1 meter to that direction. If he has the ball, he moves with it. His fatigue degree is increased by $C$ regardless of whether he has the ball or not.
- (iii) Place the ball where he stands. He loses the ball. His fatigue degree does not change.
- (iv) Take the ball. His fatigue degree does not change. A player can take this action only if he stands at the same place as the ball, and nobody has the ball.
Note that it is possible for a player or a ball to leave the field. More than one players can stand at the same place.
Since the players just finished the practice, their fatigue degrees must not be increased too much. You want to calculate the minimum possible value of the sum of fatigue degrees of the players for the clearance process.
Task
Given the size of the field and the positions of the players, write a program which calculates the minimum possible value of the sum of fatigue degrees of the players for the clearance process.
Input
Read the following data from the standard input.
- The first line of input contains two space separated integers $H$, $W$. This means the field is a rectangle whose height is $H$ meters and width is $W$ meters.
- The second line contains three space separated integers $A$, $B$, $C$ describing the increment of the fatigue degree by actions.
- The third line contains an integer N, the number of players.
- The $i$-th line ($1 \leq i \leq N$) of the following $N$ lines contains two space separated integers $S_i$, $T_i$. This means, in the beginning of the clearance, the player $i$ ($1 \leq i \leq N$) stands at ($S_i, T_i$).
Output
Write one line to the standard output. The output contains the minimum possible value of the sum of fatigue degrees of the players for the clearance process.
Constraints
All input data satisfy the following conditions.
- $1 \leq H \leq 500.$
- $1 \leq W \leq 500.$
- $0 \leq A \leq 1 000 000 000.$
- $0 \leq B \leq 1 000 000 000.$
- $0 \leq C \leq 1 000 000 000.$
- $2 \leq N \leq 100 000.$
- $0 \leq S_i \leq H (1 \leq i \leq N).$
- $0 \leq T_i \leq W (1 \leq i \leq N).$
- $(S_1, T_1) \ne (S_N, T_N).$
Sample Input and Output
Sample Input 1
6 5 1 3 6 3 1 1 0 4 6 5
Sample Output 1
26
In this sample input, the initial status of the field is as in the following figure. The white circles are the players. The black circle is the ball. You stand at (6, 5).
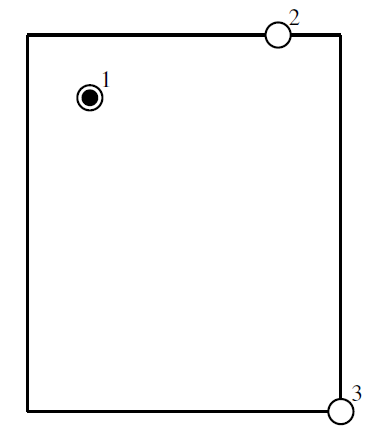
The initial status of the field
The players act as follows:
- . The player 1 kicks the ball to the east for $3$ meters. His fatigue degree is increased by $1 \times 3 + 3 = 6$. The ball moves to ($1, 4$).
- The player 2 moves $1$ meter to the south, and he has the ball. His fatigue degree is increased by $6$.
- The player 2 moves $1$ meter to the east. His fatigue degree is increased by $6$.
- The player 2 kicks the ball to the south for $5$ meters. His fatigue degree is increased by $1 \times 5 + 3 = 8$. The ball moves to ($6, 5$).
In these actions, the sum of fatigue degrees is $6 + 6 + 6 + 8 = 26$, which is the minimum possible value.
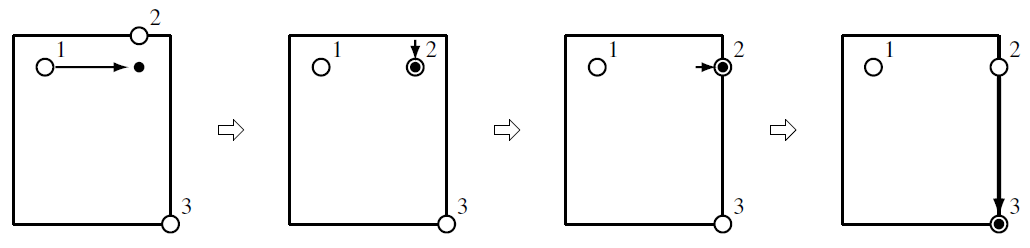
The actions in an optimal solution
Sample Input 2
3 3 0 50 10 2 0 0 3 3
Sample Output 2
60
In Sample Input 2, it not not necessary to
Sample Input 3
4 3 0 15 10 2 0 0 4 3
Sample Output 3
45
Sample Input 4
4 6 0 5 1000 6 3 1 4 6 3 0 3 0 4 0 0 4
Sample Output 4
2020
that more than one players can stand at the same place.
