Problem H: Fibonacci Sets

Fibonacci number f(i) appear in a variety of puzzles in nature and math, including packing problems, family trees or Pythagorean triangles. They obey the rule f(i) = f(i - 1) + f(i - 2), where we set f(0) = 1 = f(-1).

Let V and d be two certain positive integers and be N ≡ 1001 a constant. Consider a set of V nodes, each node i having a Fibonacci label F[i] = (f(i) mod N) assigned for i = 1,..., V ≤ N. If |F(i) - F(j)| < d, then the nodes i and j are connected.

Given V and d, how many connected subsets of nodes will you obtain?

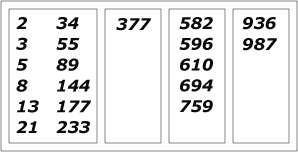
Figure 1: There are 4 connected subsets for V = 20 and d = 100.

Input

Each data set is defined as one line with two integers as follows:

Line 1: Number of nodes V and the distance d.

Input includes several data sets (i.e., several lines). The number of dat sets is less than or equal to 50.

Constraints

• 1 ≤ V ≤ 1000
• 1 ≤ d ≤ 150

Output

Output line contains one integer - the number of connected subsets - for each input line.

Sample Input

5 5
50 1
13 13

Output for the Sample Input

2
50
8

---