Problem 09: Building Houses
この秋、割火ハウスは最近開拓が進んでいる松短地区の神暗通り沿いの土地を分譲することにした。 先日募集をかけ、今日は購入者に分譲説明会を開催する。
購入者が説明会場に集まりだしたところ、なんだか空気がとても凍り付いていた。不思議に思った担当者は開催前に
「皆さん新天地を求めてきたというのに、ちょっと表情が暗いですが大丈夫ですか?」
と聞いてみた。そこで思わぬ事実が判明した。実は、購入者全員が現在隣町の集合団地の住人で、あまりにも周辺の人たちと折り合いが合わないため今回引越しをしようと検討していたのだった。
購入者たちはすでに費用を支払済みで以前の住まいを引き払っている。従って、今回分譲した松短地区の神暗通りに家を立てる他方法はない。
しかしながら、少しでも快適な新居ライフを送ってもらおうと担当者は頭を悩ませた。よくよく話を聞いてみると、仲の悪さにはバラツキがあったので、聞き込みを行い図1のような仲の悪い度チェック表を作成した:
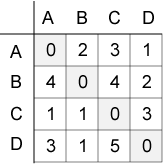
図1:仲の悪い度チェック表
購入者の数を n とすると、表は n × n の行列となり、要素 ai,j は、購入者 i が自分の家から購入者 j の家を最低でも何 m 離したいかを示す。例えば、図1の表において、購入者 A は自分の家と購入者 B の家の距離が 2 m 以上離れていないと納得しない。さらに、購入者 B は自分の家と購入者 A の家の距離が 4 m 以上離れていないと納得しない。従って A と B の距離は 4 m 以上離す必要がある。
担当者はこの表に基づき隣の家との間隔を設け土地のレイアウトを設計することにした。
あなたの仕事は、仲の悪い度チェック表を入力し、購入者の家を神暗通り(一直線上)に建てるために最低限必要な通りの長さ(m)を出力するプログラムを作成することである。 なお簡単のために、家は点として扱い、その幅は 0 m と仮定する。
Input
入力として複数のデータセットが与えられる。各データセットは以下の形式で与えられる:
n (購入者の数:整数)
a1,1 a1,2 ... a1,n (a1,j:整数)
a2,1 a2,2 ... a2,n (a2,j:整数)
.
.
an,1 an,2 ... an,n (an,j:整数)
n は 10 以下とする。ai,i は 0 であり、ai,j (i ≠ j) は 1 以上である。
n が 0 のとき入力の終わりとする。
Output
各データセットについて、最低限必要な通りの長さを1行に出力せよ。
Sample Input
4 0 2 3 1 4 0 4 2 1 1 0 3 3 1 5 0 2 0 3 3 0 0
Output for the Sample Input
8 3