Problem F: Cutting a Chocolate

Turtle Shi-ta and turtle Be-ko decided to divide a chocolate. The shape of the chocolate is rectangle. The corners of the chocolate are put on (0,0), (w,0), (w,h) and (0,h). The chocolate has lines for cutting. They cut the chocolate only along some of these lines.

The lines are expressed as follows. There are m points on the line connected between (0,0) and (0,h), and between (w,0) and (w,h). Each i-th point, ordered by y value (i = 0 then y =0), is connected as cutting line. These lines do not share any point where 0 < x < w . They can share points where x = 0 or x = w . However, (0, l_i ) = (0,l_j ) and (w,r_i ) = (w,r_j ) implies i = j . The following figure shows the example of the chocolate.

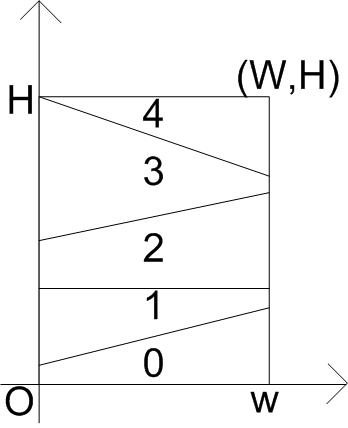
There are n special almonds, so delicious but high in calories on the chocolate. Almonds are circle but their radius is too small. You can ignore radius of almonds. The position of almond is expressed as (x,y) coordinate.

Two turtles are so selfish. Both of them have requirement for cutting.

Shi-ta's requirement is that the piece for her is continuous. It is possible for her that she cannot get any chocolate. Assume that the minimum index of the piece is i and the maximum is k . She must have all pieces between i and k . For example, chocolate piece 1,2,3 is continuous but 1,3 or 0,2,4 is not continuous.

Be-ko requires that the area of her chocolate is at least S . She is worry about her weight. So she wants the number of almond on her chocolate is as few as possible.

They doesn't want to make remainder of the chocolate because the chocolate is expensive.

Your task is to compute the minumum number of Beko's almonds if both of their requirment are satisfied.

Input

Input consists of multiple test cases.
Each dataset is given in the following format.

n m w h S
l0 r0
...
lm-1 rm-1
x0 y0
...
xn-1 yn-1

The last line contains five 0s. n is the number of almonds. m is the number of lines. w is the width of the chocolate. h is the height of the chocolate. S is the area that Be-ko wants to eat. Input is integer except x_i y_i.

Input satisfies following constraints.
1 ≤ n ≤ 30000
1 ≤ m ≤ 30000
1 ≤ w ≤ 200
1 ≤ h ≤ 1000000
0 ≤ S ≤ w*h

If i < j then l_i ≤ l_j and r_i ≤ r_j and then i -th lines and j -th lines share at most 1 point. It is assured that l_m-1 and r_m-1 are h. x_i y_i is floating point number with ten digits. It is assured that they are inside of the chocolate. It is assured that the distance between points and any lines is at least 0.00001.

Output

You should output the minumum number of almonds for Be-ko.

Sample input

2 3 10 10 50
3 3
6 6
10 10
4.0000000000 4.0000000000
7.0000000000 7.0000000000
2 3 10 10 70
3 3
6 6
10 10
4.0000000000 4.0000000000
7.0000000000 7.0000000000
2 3 10 10 30
3 3
6 6
10 10
4.0000000000 4.0000000000
7.0000000000 7.0000000000
2 3 10 10 40
3 3
6 6
10 10
4.0000000000 4.0000000000
7.0000000000 7.0000000000
2 3 10 10 100
3 3
6 6
10 10
4.0000000000 4.0000000000
7.0000000000 7.0000000000
0 0 0 0 0

Sample output

1
1
0
1
2

---