Spiral Footrace

Let us enjoy extraordinary footraces at an athletic field. Before starting the race, small flags representing checkpoints are set up at random on the field. Every runner has to pass all the checkpoints one by one in the spiral order specified below. The starting point is the southwest corner of the athletic field.

At the starting point, runners are facing north. During the race, they run clockwise in a spiral passing every checkpoint as illustrated in the following figure. When moving from one flag to the next, they take a straight path. This means that the course of a race is always piecewise linear.

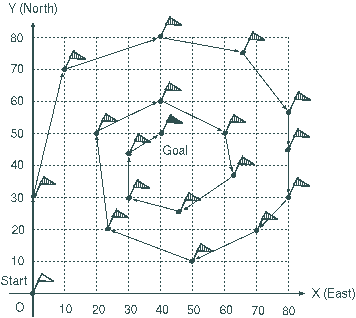
Upon arriving at some flag, a runner has to determine the next flag among those that are not yet visited. That flag shall be the one at the smallest angle to the right of the direction that the runner is facing. When more than two flags are on the same straight line, the runner visits the nearest flag first. The goal position is the place of the last visited flag.

Your job is to write a program that calculates the length of the course from the starting point to the goal, supposing that the course consists of line segments connected by flags. The position of each flag is given by a coordinate pair (x_i, y_i), which is limited to the first quadrant. The starting point is fixed to the origin (0, 0) where a flag is always set up.

Input

The input contains multiple data sets, each representing a collection of flag positions for a footrace. A data set is given in the following format.

n
x₁ y₁
x₂ y₂
...
x_n y_n

Here, n is the number of flag positions (1 <= n <= 400). The position of the i-th flag is given by (x_i, y_i), where x_i and y_i are integers in meter between 0 and 500 inclusive. There may be white spaces (blanks and/or tabs) before, in between, or after x_i and y_i. Once a certain coordinate pair (x_i, y_i) is given, the same one will not appear later in the data set, and the origin (0, 0) will not appear either.

A data set beginning with n = 0 indicates end of the input.

Output

For each data set, your program should output the length of the running course in meter. Each length should appear on a separate line, with one digit to the right of the decimal point, after rounding it to one decimal place.

Sample Input

8
   60  70
   20  40
   50  50
   70  10
   10  70
   80  90
   70  50
  100  50
5
   60  50
    0  80
   60  20
   10  20
   60  80
0

Output for the Sample Input

388.9
250.0

---