Patience

As the proverb says,

"Patience is bitter, but its fruit is sweet."

Writing programs within the limited time may impose some patience on you, but you enjoy it and win the contest, we hope.

The word "patience" has the meaning of perseverance, but it has another meaning in card games. Card games for one player are called "patience" in the UK and "solitaire" in the US.

Let's play a patience in this problem.

In this card game, you use only twenty cards whose face values are positive and less than or equal to 5 (Ace's value is 1 as usual). Just four cards are available for each face value.

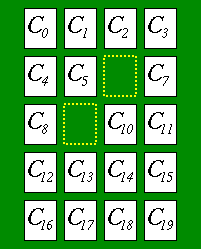
At the beginning, the twenty cards are laid in five rows by four columns (See Figure 1). All the cards are dealt face up.

An example of the initial layout is shown in Figure 2.

Figure 1: Initial layout	Figure 2: Example of the initial layout

The purpose of the game is to remove as many cards as possible by repeatedly removing a pair of neighboring cards of the same face value. Let us call such a pair a matching pair.

The phrase "a pair of neighboring cards" means a pair of cards which are adjacent to each other. For example, in Figure 1, C₆ is adjacent to any of the following eight cards:

C₁, C₂, C₃, C₅, C₇, C₉, C₁₀ and C₁₁. In contrast, C₃ is adjacent to only the following three cards: C₂, C₆ and C₇.

Every time you remove a pair, you must rearrange the remaining cards as compact as possible.
To put it concretely, each remaining card C_i must be examined in turn in its subscript order to be shifted to the uppermost-leftmost space.

How to play:

1. Search a matching pair.
2. When you find more than one pair, choose one.
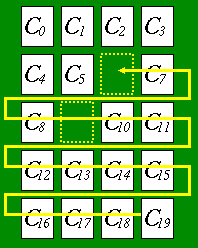
   In Figure 3, you decided to remove the pair of C₆ and C₉.
3. Remove the pair. (See Figure 4)
4. Shift the remaining cards to the uppermost-leftmost space (See Figure 5, 6).
5. Repeat the above procedure until you cannot remove any pair.

Figure 3: A matching pair found	Figure 4: Remove the matching pair

Figure 5: Shift the remaining cards	Figure 6: Rearranged layout

If you can remove all the twenty cards, you win the game and your penalty is 0. If you leave some cards, you lose the game and your penalty is the number of the remaining cards.

Whenever you find multiple matching pairs, you must choose one pair out of them as in the step 2 of the above procedure. The result of the game depends on these choices.

Your job is to write a program which answers the minimal penalty for each initial layout.

Input

The input consists of multiple card layouts. The input is given in the following format.

        N
        Layout0
        Layout1
        ...
        LayoutN-1

N is the number of card layouts. Each card layout gives the initial state of a game. A card layout is given in the following format.

        C0   C1   C2   C3
        C4   C5   C6   C7
        C8   C9   C10  C11
        C12  C13  C14  C15
        C16  C17  C18  C19

C_i (0 <= i <= 19) is an integer from 1 to 5 which represents the face value of the card.

Output

For every initial card layout, the minimal penalty should be output, each in a separate line.

Sample Input

4
1 4 5 2
3 1 4 3
5 4 2 2
4 5 2 3
1 1 3 5
5 1 5 1
4 5 3 2
3 2 1 4
1 4 5 3
2 3 4 2
1 2 1 2
5 4 5 4
2 1 2 1
3 5 3 4
3 3 5 4
4 2 3 1
2 5 3 1
3 5 4 2
1 5 4 1
4 5 3 2

Output for the Sample Input

0
4
12
0

---