Strange Key
Professor Tsukuba invented a mysterious jewelry box that can be opened with a special gold key whose shape is very strange. It is composed of gold bars joined at their ends. Each gold bar has the same length and is placed parallel to one of the three orthogonal axes in a three dimensional space, i.e., x-axis, y-axis and z-axis.
The locking mechanism of the jewelry box is truly mysterious, but the shape of the key is known. To identify the key of the jewelry box, he gave a way to describe its shape.
The description indicates a list of connected paths that completely defines the shape of the key: the gold bars of the key are arranged along the paths and joined at their ends. Except for the first path, each path must start from an end point of a gold bar on a previously defined path. Each path is represented by a sequence of elements, each of which is one of six symbols (+x, -x, +y, -y, +z and -z) or a positive integer. Each symbol indicates the direction from an end point to the other end point of a gold bar along the path. Since each gold bar is parallel to one of the three orthogonal axes, the 6 symbols are enough to indicate the direction. Note that a description of a path has direction but the gold bars themselves have no direction.
An end point of a gold bar can have a label, which is a positive integer. The labeled point may be referred to as the beginnings of other paths. In a key description, the first occurrence of a positive integer defines a label of a point and each subsequent occurrence of the same positive integer indicates the beginning of a new path at the point.
An example of a key composed of 13 gold bars is depicted in Figure 1.
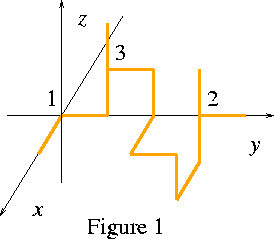
The following sequence of lines
19
1 +x 1 +y +z 3 +z
3 +y -z +x +y -z -x +z 2 +z
2 +y
is a description of the key in Figure 1. Note that newlines have the same role as space characters in the description, so that "19 1 +x 1 +y +z 3 +z 3 +y -z +x +y -z -x +z 2 +z 2 +y" has the same meaning.
The meaning of this description is quite simple. The first integer "19" means the number of the following elements in this description. Each element is one of the 6 symbols or a positive integer.
The integer "1" at the head of the second line is a label attached to the starting point of the first path. Without loss of generality, it can be assumed that the starting point of the first path is the origin, i.e., (0,0,0), and that the length of each gold bar is 1. The next element "+x" indicates that the first gold bar is parallel to the x-axis, so that the other end point of the gold bar is at (1,0,0). These two elements "1" and "+x" indicates the first path consisting of only one gold bar. The third element of the second line in the description is the positive integer "1", meaning that the point with the label "1", i.e., the origin (0,0,0) is the beginning of a new path. The following elements "+y", "+z", "3", and "+z" indicate the second path consisting of three gold bars. Note that this "3" is its first occurrence so that the point with coordinates (0,1,1) is labeled "3". The head of the third line "3" indicates the beginning of the third path and so on. Consequently, there are four paths by which the shape of the key in Figure 1 is completely defined.
Note that there are various descriptions of the same key since there are various sets of paths that cover the shape of the key. For example, the following sequence of lines
19
1 +x 1 +y +z 3 +y -z +x +y -z -x +z 2 +y
3 +z
2 +z
is another description of the key in Figure 1, since the gold bars are placed in the same way.
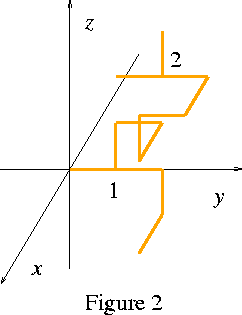
Furthermore, the key may be turned 90-degrees around x-axis, y-axis or z-axis several times and may be moved parallelly. Since any combinations of rotations and parallel moves don't change the shape of the key, a description of a rotated and moved key also represent the same shape of the original key. For example, a sequence
17
+y 1 +y -z +x
1 +z +y +x +z +y -x -y 2 -y
2 +z
is a description of a key in Figure 2 that represents the same key as in Figure 1. Indeed, they are congruent under a rotation around x-axis and a parallel move.
Your job is to write a program to judge whether or not the given two descriptions define the same key.
Note that paths may make a cycle. For example, "4 +x +y -x -y" and "6 1 +x 1 +y +x -y" are valid descriptions. However, two or more gold bars must not be placed at the same position. For example, key descriptions "2 +x -x" and "7 1 +x 1 +y +x -y -x" are invalid.
Input
An input data is a list of pairs of key descriptions followed by a zero that indicates the end of the input. For p pairs of key descriptions, the input is given in the following format.
-
key-description1-a
key-description1-b
key-description2-a
key-description2-b
...
key-descriptionp-a
key-descriptionp-b
0
Each key description (key-description) has the following format.
-
n
e1 e2
...
ek
...
en
The positive integer n indicates the number of the following elements e1, ..., en . They are separated by one or more space characters and/or newlines. Each element ek is one of the six symbols (+x, -x, +y, -y, +z and -z) or a positive integer.
You can assume that each label is a positive integer that is less than 51, the number of elements in a single key description is less than 301, and the number of characters in a line is less than 80. You can also assume that the given key descriptions are valid and contain at least one gold bar.
Output
The number of output lines should be equal to that of pairs of key descriptions given in the input. In each line, you should output one of two words "SAME", when the two key descriptions represent the same key, and "DIFFERENT", when they are different. Note that the letters should be in upper case.
Sample Input
19 1 +x 1 +y +z 3 +z 3 +y -z +x +y -z -x +z 2 +z 2 +y 19 1 +x 1 +y +z 3 +y -z +x +y -z -x +z 2 +y 3 +z 2 +z 19 1 +x 1 +y +z 3 +z 3 +y -z +x +y -z -x +z 2 +y 2 +z 18 1 -y 1 +y -z +x 1 +z +y +x +z +y -x -y 2 -y 2 +z 3 +x +y +z 3 +y +z -x 0
Output for the Sample Input
SAME SAME DIFFERENT