Problem D: 崖登り
17:00, 特別捜査官 Jack が敵のキャンプから脱出を開始した. 最寄りの安全地帯に逃れるには,途中にある崖を登る必要がある. その急な崖はブロックで覆われており, Jack はブロックに足を置きながら崖を登ることになる. 表面が滑りやすいブロックに進むには時間をかける必要があり, もろいブロックは体重で崩れてしまうので避ける必要がある. あなたの使命は,崖を登りきるために必要な最短の時間を求めるプログラムを作成することである.
図 D-1 は,あなたが受け取るであろう崖に関する地形データの例を図示したものである. 崖は,正方形のブロックで覆われており, Jack の崖登りは, 崖下の地面から, 一番下の段の 'S' とマークされたブロックに片足を置くことで開始される. 最初のステップは,左右のどちらの足であっても良い. ブロックにマークされた数字は,そのブロックの「滑りやすさ」を意味する. t (1 ≤ t ≤ 9) とマークされたブロックに足を安全に置くには, t 単位時間が必要となる. 'X' でマークされたブロックには Jack は足を置くことはできない. どちらかの足が,最上段の 'T' とマークされたブロックに到着した時点で崖登り完了で ある.

図 D-1: 崖に関するデータの例
Jack は,崖登りにおいて以下の制約をうける. 左足を動かした次は右足を,右足を動かした次は左足を動かすこと. 左足の座標 (lx, ly)と 右足の座標 (rx, ry) に関し, lx < rx 及び | lx - rx | + | ly - ry | ≤ 3 が成り立つこと. つまり,左足が図 D-2 (a) の位置にある場合は, 青色で示された9つの位置にしか右足を置くことができない. 同様に,右足が図 D-2 (b) の位置にある場合も, 青色で示された9つの位置にしか左足を置くことができない.
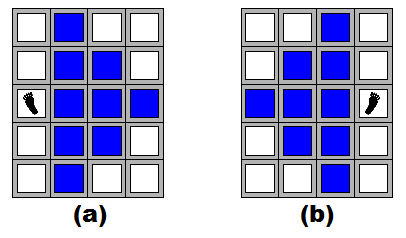
図 D-2: 可能な足の配置
Input
入力は,複数のデータセットからなり, 入力の終わりはスペースで区切られたゼロ二つからなる行である. 各データセットは,次の形式をしている.
w h
s(1,1) ... s(1,w)
s(2,1) ... s(2,w)
...
s(h,1) ... s(h,w)
w と h は,それぞれ崖を表現する行列データの幅と高さを示す整数であり, それぞれ2 ≤ w ≤ 30, 5 ≤ h ≤ 60 と仮定して良い. 続く h 行はそれぞれ,スペースで区切られた w 個の文字から構成されており, 文字s(y,x) は,座標 (x, y)のブロックの状態を示す. その意味は,以下の通り:
- 'S': Jack が崖登りを開始可能なブロック.
- 'T': Jack が崖登りを終了可能なブロック.
- 'X': Jack が足を置くことができないブロック.
- '1'-'9' (= t): Jack がどちらかの足を置く際に, t 単位時間を必要とするブロック.
'S' や 'T' でマークされたブロックに足を置くための時間は,0 と考えてよい.
Output
各データセットについて,崖登りに必要な最小時間を求め, 十進の整数値として,それぞれ1行に出力しなさい. 崖登りを完了できない場合は,代わりに -1 のみを含む行を出力しなさい. 各出力行はこれらの数値以外の文字を含んではならない.
Sample Input
6 6 4 4 X X T T 4 7 8 2 X 7 3 X X X 1 8 1 2 X X X 6 1 1 2 4 4 7 S S 2 3 X X 2 10 T 1 1 X 1 X 1 X 1 1 1 X 1 X 1 1 1 X S S 2 10 T X 1 X 1 X 1 X 1 1 1 X 1 X 1 1 1 X S S 10 10 T T T T T T T T T T X 2 X X X X X 3 4 X 9 8 9 X X X 2 9 X 9 7 7 X 7 3 X X 8 9 X 8 9 9 9 6 3 X 5 X 5 8 9 9 9 6 X X 5 X 5 8 6 5 4 6 8 X 5 X 5 8 9 3 9 6 8 X 5 X 5 8 3 9 9 6 X X X 5 X S S S S S S S S S S 10 7 2 3 2 3 2 3 2 3 T T 1 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 2 3 4 3 2 3 2 3 2 3 2 3 5 3 2 3 1 3 2 3 2 3 5 2 2 3 2 4 2 3 2 3 5 S S 2 3 2 1 2 3 2 3 0 0
Output for the Sample Input
12 5 -1 22 12