Problem C: 如何に汝を満足せしめむ? いざ数え上げむ…
三値論理は値として "真","偽" に加え "未知" を許す論理体系である. 以下では,"偽","未知","真" を 0, 1, 2 でそれぞれ表す.
"-" を単項演算子(すなわち,値ひとつを受け取る関数を表す記号)とし, "*" と "+" を二項演算子(すなわち,値ふたつを受け取る関数を表す記号)とする. これらは,それぞれ否定 (NOT), 論理積 (AND), 論理和 (OR) を表す演算子であり, 三値論理におけるこれらの演算は表 C-1 に示すように定義できる.
| -X | (X*Y) | (X+Y) | |||
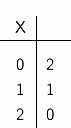 | 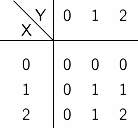 | 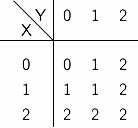 |
P, Q, R を三値論理の変数とする. 与えられた論理式を満足する, つまり論理式の値が 2 になるような (P,Q,R) の三つ組が何通りあるかを答えるのがあなたの役割だ. 論理式は以下のいずれかの形式である(ここで X, Y はまた論理式であるとする).
- 定数: 0, 1 または 2
- 変数: P, Q または R
- 否定: -X
- 論理積: (X*Y)
- 論理和: (X+Y)
上記のように,ふたつの論理式の論理積や論理和は必ず括弧で囲む.
たとえば,入力 (P*Q) に対しては,(P,Q,R) が (2,2,0),(2,2,1),(2,2,2) の場合, かつその場合のみ,この論理式の値が 2となるので,3を出力すればよい.
Input
入力は ひとつ以上の行からなり,入力の各行は論理式ひとつを含む. 論理式は 0, 1, 2, P, Q, R, -, *, +, (, ) から成る文字列であり, 空白など他の文字を含まない.論理式の文法は次の BNF で与えられる.
<formula> ::= 0 | 1 | 2 | P | Q | R |
-<formula> | (<formula>*<formula>) | (<formula>+<formula>)
すべての論理式はこの構文規則に従うので,文法エラーを気にする必要はない. 入力行の長さは 80文字を超えない.
入力の終わりは "."(ピリオド)ひとつだけからなる行によって示される.
Output
入力の論理式の値を 2 とするような (P,Q,R) の三つ組の個数を十進数で出力せよ. 出力は論理式ひとつごとに 1 行とし, 各行は個数を表す十進数以外の文字を含んではならない.
Sample Input
(P*Q) (--R+(P*Q)) (P*-P) 2 1 (-1+(((---P+Q)*(--Q+---R))*(-R+-P))) .
Output for the Sample Input
3 11 0 27 0 7