Problem D: ぐらぐら
あなたの勤め先のピカソニアン・キュービズム国際センター(ICPC)の事務局では,若き芸術家のための美術館を新たに建設する.そのためセンターでは建物の設計コンペを開催することになった.
コンペに提出される図面は,下に示すように,かの有名なゲームの画面のようなものになる.
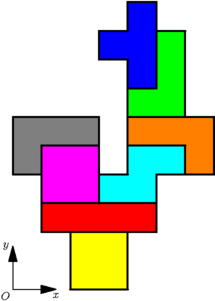
それというのも,センターが指定する工法が「ピース」と呼ばれる規格化されたユニットを積み重ねて建築するというものだからである.各ピースは4つの立方体のブロックをつなげて作られている.センターはさらに,応募される設計に次のような条件を課している.
- ピースはブロック単位で位置を揃えてある.つまりピースとピースが接する場合,両者のブロックの面どうしはぴったり重なるような置き方しか許されない.
- ピースは安定していなければいけない.ピースは積み重ねられるだけなので,崩れてしまわないように重心の位置を慎重に定めなければいけない.
- ピースは樹状に積み重ねられ,それによって若き芸術家達の無限の可能性を象徴する.つまり,地面に接しているピースは唯1つだけで,それ以外の各ピースの下面が接しているピースは丁度1つだけに限られている.
- 建物は平らな形に限られる.これは建設予定地が下図に示すようなお堀と高速道路にはさまれた狭い所で,お堀と高速道路の間にはブロック1個分の幅しかないためである.
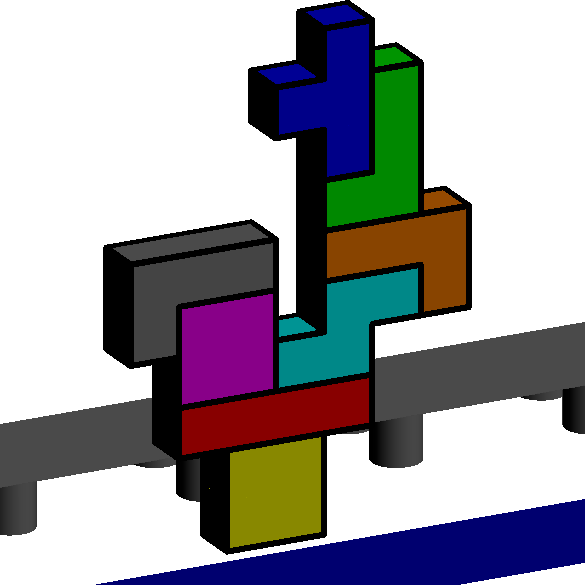
建物の安定性を完全に調べるには,複雑な構造計算が必要なため何日もかかる.そこであなたは安定性の簡易診断を行うことを命じられた.簡易診断の方法は次のようである.
以下では各ブロックの重心はブロックの中心にあり,全てのブロックは同じ重さだと仮定する.また,ブロックの位置をブロックの左下のxy座標によって表す.単位はブロックの辺の長さである.
ピースを構成するブロックで下面が他のピースまたは地面に接しているもののうち,一番左のものの左端のx座標を xL,一番右のものの右端のx座標を xR とする.また,このピースによって直接または間接に支えられているすべてのピースとこのピース自身をあわせた全体の重心のx座標をMとする.このときxL < M < xR が成り立てばピースは安定であり,そうでなければ不安定である.建物を構成するピースが1つでも不安定であれば,その建物は不安定である.
上記の診断方法は,実際には崩れないような設計を不安定と判定する場合もあることに注意せよ.例えば,下図左の設計は不安定と判定される.
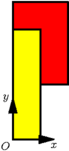 |
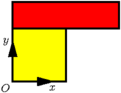 |
またこの診断方法は境界状態にある場合は不安定と判定することにも注意せよ.例えば,上図右の設計における上のピースの重心は,下のピースの右端の真上にあるが,これは不安定と判定される.
簡易診断方法によって各設計の安定性を診断するプログラムを書け.
Input
入力は複数のデータセットからなる.入力の終わりは空白1つで区切られた2個のゼロからなる行によって与えられる.各データセットは建物の正面図を表し,その形式は以下の通りである.
w h
p0(h-1)p1(h-1)...p(w-1)(h-1)
...
p01p11...p(w-1)1
p00p10...p(w-1)0
空白で区切られた整数wおよびhはそれぞれ配置の列数と行数を表す.ここで 1 ≤ w ≤
10 かつ 1 ≤ h ≤ 60 と仮定してよい.続くh行はピースの配置を与える.pxyの文字は座標(x,y)のブロックの状態を表し,何もないことを表す「.」あるいはピースを構成するブロックを表す「1」から「9」までの数字のどれかである.(すでに述べたように,ブロックの位置はブロックの左下のxy座標によって表す.)
同じ数字を持つ2つのブロックが上下あるいは左右を接している場合,それらのブロックは同一のピースの部分である.(同じ数字を持つ異なる2つのピースが有り得ることに注意せよ.)座標(x,0)にあるブロックの下面は地面に接している.
各データセットは,ピースを樹状に積み重ねているものと仮定してよい.
Output
それぞれのデータセットについて,設計が上記の条件に従って安定な場合にはSTABLE, そうでない場合はUNSTABLEと全て大文字で書かれた行を出力せよ.出力にそれ以外の文字を含めてはならない.
Sample Input
4 5 ..33 ..33 2222 ..1. .111 5 7 ....1 .1..1 .1..1 11..1 .2222 ..111 ...1. 3 6 .3. 233 23. 22. .11 .11 4 3 2222 ..11 ..11 4 5 .3.. 33.. 322. 2211 .11. 3 3 222 2.1 111 3 4 11. 11. .2. 222 3 4 .11 .11 .2. 222 2 7 11 .1 21 22 23 .3 33 2 3 1. 11 .1 0 0
Output for the Sample Input
STABLE STABLE STABLE UNSTABLE STABLE STABLE UNSTABLE UNSTABLE UNSTABLE UNSTABLE