Problem G: Laser Beam Reflections

A laser beam generator, a target object and some mirrors are placed on a plane. The mirrors stand upright on the plane, and both sides of the mirrors are flat and can reflect beams. To point the beam at the target, you may set the beam to several directions because of different reflections. Your job is to find the shortest beam path from the generator to the target and answer the length of the path.

Figure G-1 shows examples of possible beam paths, where the bold line represents the shortest one.

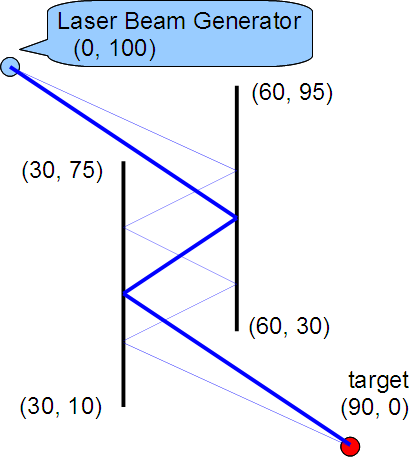
Figure G-1: Examples of possible paths

Input

The input consists of a number of datasets. The end of the input is indicated by a line containing a zero.

Each dataset is formatted as follows. Each value in the dataset except n is an integer no less than 0 and no more than 100.

n
PX₁ PY₁ QX₁ QY₁
...
PX_n PY_n QX_n QY_n
TX TY
LX LY

The first line of a dataset contains an integer n (1 ≤ n ≤ 5), representing the number of mirrors. The following n lines list the arrangement of mirrors on the plane. The coordinates (PX_i, PY_i) and (QX_i, QY_i) represent the positions of both ends of the mirror. Mirrors are apart from each other. The last two lines represent the target position (TX, TY) and the position of the beam generator (LX, LY). The positions of the target and the generator are apart from each other, and these positions are also apart from mirrors.

The sizes of the target object and the beam generator are small enough to be ignored. You can also ignore the thicknesses of mirrors.

In addition, you can assume the following conditions on the given datasets.

• There is at least one possible path from the beam generator to the target.
• The number of reflections along the shortest path is less than 6.
• The shortest path does not cross or touch a plane containing a mirror surface at any points within 0.001 unit distance from either end of the mirror.
• Even if the beam could arbitrarily select reflection or passage when it reaches each plane containing a mirror surface at a point within 0.001 unit distance from one of the mirror ends, any paths from the generator to the target would not be shorter than the shortest path.
• When the beam is shot from the generator in an arbitrary direction and it reflects on a mirror or passes the mirror within 0.001 unit distance from the mirror, the angle θ formed by the beam and the mirror satisfies sin(θ) > 0.1, until the beam reaches the 6th reflection point (exclusive).

Figure G-1 corresponds to the first dataset of the Sample Input below. Figure G-2 shows the shortest paths for the subsequent datasets of the Sample Input.

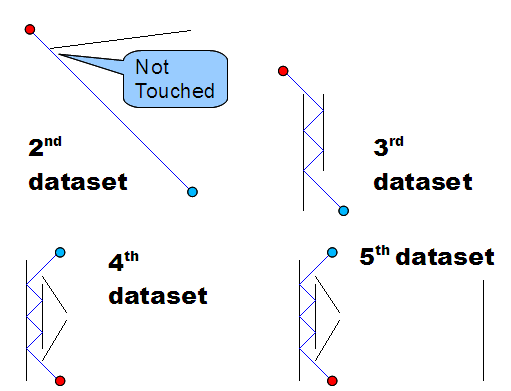
Figure G-2: Examples of the shortest paths

Output

For each dataset, output a single line containing the length of the shortest path from the beam generator to the target. The value should not have an error greater than 0.001. No extra characters should appear in the output.

Sample Input

2
30 10 30 75
60 30 60 95
90 0
0 100
1
20 81 90 90
10 90
90 10
2
10 0 10 58
20 20 20 58
0 70
30 0
4
8 0 8 60
16 16 16 48
16 10 28 30
16 52 28 34
24 0
24 64
5
8 0 8 60
16 16 16 48
16 10 28 30
16 52 28 34
100 0 100 50
24 0
24 64
0

Output for the Sample Input

180.27756377319946
113.13708498984761
98.99494936611666
90.50966799187809
90.50966799187809

---