正方形の部屋を縦横に並べた長方形領域の迷路がある．この迷路は出入口を除いて壁で囲まれている．迷路の入口は長方形の上辺の最も左側で，つまり最上段の最左の部屋の上辺は開いている．出口は同様に下辺の最も右側にある．

迷路の中で，ある部屋と縦または横に隣り合う部屋との間には壁があり，カードキーで開けられるドアが1つあるか全くドアがないかのどちらかである．ドアがある場合は，カードを1枚入れるとドアが開いて通り抜けることができるが，ドアはすぐに閉まり，カードは返却されない．カードは1種類でどこのドアでも使うことができる．ドアがない壁を通り抜けることはできない．

迷路の地図が与えられた時に，カードが何枚あれば入口から出口に抜けられるかを求めるのは簡単な問題だろう．図G-1の場合は，図G-2の緑の矢印()の経路を辿れば，10枚のカードで抜けられることが分かる．

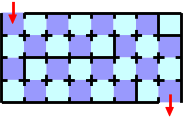
図 G-1: 迷路の地図

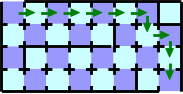
図 G-2: 最短経路

迷路中のドアが一箇所だけ故障していて通れなくなっていることが分かった． どこのドアが故障しているかの情報はない．壊れたドアにカードを入れるとカードは直ちに返却される．ドアの故障は見ただけでは分からない．

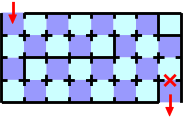
図 G-3: 通り抜けられなくなる可能性のある迷路

図G-3の場合，故障しているドアが赤いバツ印() の位置のドアの場合は入口から出口に行けなくなるが，図G-1の迷路では故障しているドアがどれであっても，入口から出口に行くことはできる．図G-1 の迷路で，図G-2の最短経路を行こうとして図G-4の赤いバツ印のドアが故障していることを発見した場合，緑の矢印の経路で出口にたどり着くことになるだろう．この場合，カードは20枚必要になる．

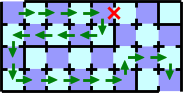
図 G-4: ドアが故障した迷路

しかし，この迷路はもっと少ない枚数のカードで抜けることができる．まず，ドアの故障を見つけるまでは図G-5の経路にしたがって進む．これは故障がなくても12枚のカードが必要なので最短経路ではない．経路の途中で故障しているドアを見つけたら，そこからそのドアを使わないときの出口への最短経路で進む．この戦略ならば故障しているドアがどこであっても16枚のカードで抜けることができる．この戦略で最悪となる16枚のカードが必要なケースを図G-6に示す．

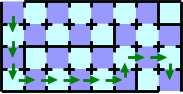
図 G-5: 故障発見前の経路

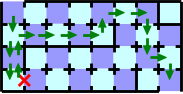
図 G-6: 16枚のカードが必要な例

迷路の地図を与えられた時に，故障したドアがどこであっても迷路を抜けることのできるカードの枚数の最小値を答えるプログラムを作成しなさい．

入力はそれぞれが迷路を表すひとつ以上のデータセットからなる．データセット数は100以下である．

データセットの最初の行には迷路の高さ hと幅 w を与えるふたつの整数値がこの順に入っている．2 ≤ h, w ≤ 30 であるものとしてよい．

それに続く 2 × h − 1 行は，隣接する部屋の間のドアの有無を示している．最初の行の先頭は空白で，その後には w − 1 個の 1 または 0 が空白ひとつで区切られて並んでいる．これらは一番上の行の横に隣り合う部屋の間のドアの有無を示すものである．1 はドアがないことを，0 はあることを意味する． 次の行の先頭には空白はなく，w 個の 1 または 0 が空白ひとつを区切りに続く．これらは最初と次の行の縦に隣り合う部屋の間のドアの有無を表す．整数 0/1 はドアの有/無を示す．引き続く行は交互に横と縦に隣り合う部屋の間のドアの有無を同様に表す．

入力の終わりはふたつのゼロを含む行で表される．

各データセットについて，必要なカードの枚数の最小値を表す整数ひとつを持 つ行を出力せよ．また，故障しているドアによって入口から出口へ行く経路がなくな る可能性のある場合は −1 を出力せよ．出力行にはこの数値以外の文字を 含んではならない．

4 8
 0 0 0 0 0 0 1
0 0 0 0 0 0 0 1
 0 0 0 0 1 0 0
0 1 1 1 1 0 0 0
 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0
 0 0 0 0 0 1 0
4 8
 0 0 0 0 0 0 1
0 0 0 0 0 0 0 1
 0 0 0 0 1 0 0
0 1 1 1 1 0 0 0
 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0
 0 0 0 0 0 0 1
2 2
 0
0 0
 0
3 3
 0 0
0 1 0
 0 1
0 0 0
 0 0
2 4
 1 0 1
0 0 0 0
 0 1 0
6 12
 0 0 0 1 1 0 0 0 0 0 0
0 1 1 0 0 0 0 0 0 1 1 0
 1 0 0 1 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0
 1 0 0 1 1 0 0 1 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0
 1 0 0 1 1 0 0 1 1 0 0
0 0 0 1 0 0 0 0 0 0 0 0
 0 0 0 0 1 0 0 1 1 0 0
0 0 0 0 0 1 1 0 0 1 0 0
 1 0 0 0 0 0 0 1 0 0 0
20 20
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0

16
-1
4
10
-1
32
40