Integral Rectangles

Let us consider rectangles whose height, h, and width, w, are both integers. We call such rectangles integral rectangles. In this problem, we consider only wide integral rectangles, i.e., those with w > h.

We define the following ordering of wide integral rectangles. Given two wide integral rectangles,

1. The one shorter in its diagonal line is smaller, and
2. If the two have diagonal lines with the same length, the one shorter in its height is smaller.

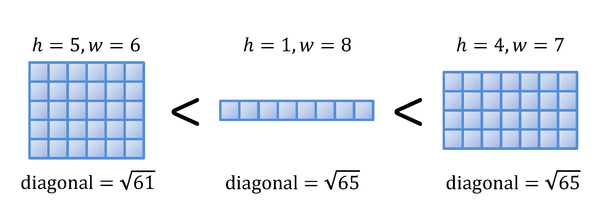
Given a wide integral rectangle, find the smallest wide integral rectangle bigger than the given one.

Input

The entire input consists of multiple datasets. The number of datasets is no more than 100. Each dataset describes a wide integral rectangle by specifying its height and width, namely h and w, separated by a space in a line, as follows.

h w

For each dataset, h and w (>h) are both integers greater than 0 and no more than 100.

The end of the input is indicated by a line of two zeros separated by a space.

Output

For each dataset, print in a line two numbers describing the height and width, namely h and w (> h), of the smallest wide integral rectangle bigger than the one described in the dataset. Put a space between the numbers. No other characters are allowed in the output.

For any wide integral rectangle given in the input, the width and height of the smallest wide integral rectangle bigger than the given one are both known to be not greater than 150.

In addition, although the ordering of wide integral rectangles uses the comparison of lengths of diagonal lines, this comparison can be replaced with that of squares (self-products) of lengths of diagonal lines, which can avoid unnecessary troubles possibly caused by the use of floating-point numbers.

Sample Input

1 2
1 3
2 3
1 4
2 4
5 6
1 8
4 7
98 100
99 100
0 0

Output for the Sample Input

1 3
2 3
1 4
2 4
3 4
1 8
4 7
2 8
3 140
89 109

---