円を横切るな！

平面上に 1 つ以上の円が配置されている． 任意の 2 つの円は，中心位置と半径の両方もしくは一方が異なる． 円は，他の円と共通領域をもつことはあるが， 3 つ以上の円が共通領域もしくは共通点をもつことはない． 円が，他の円を含むことや，2 点で交差することはあるが， 2 つの円の円周が 1 点で接することはないと仮定してよい．

あなたの仕事は，指定された 2 点 P と Q を結ぶようなパスで，どの円弧とも交差しないものが存在するか，答えることである． 円の配置に対して，点の組は 1 組以上与えられる．

Figure G-1 の例では，円弧と交差することなく P と Q₁ を結ぶことはできるが，円弧と交差することなく P と Q₂, Q₃, Q₄ を結ぶことはできない．

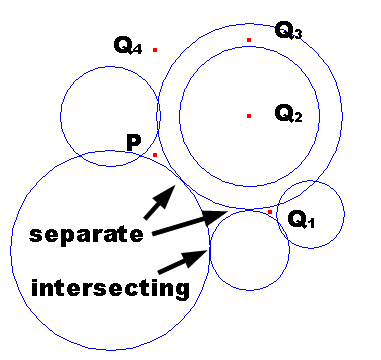
図 G-1: 円および点の配置例

Input

入力は複数のデータセットからなり， 各データセットは次の形式で表される．

n m
Cx₁ Cy₁ r₁
...
Cx_n Cy_n r_n
Px₁ Py₁ Qx₁ Qy₁
...
Px_m Py_m Qx_m Qy_m

データセットの最初の行は， 空白文字 1 個で区切られた 2 個の整数 n, m からなる． n は，円の個数であり，1 ≤ n ≤ 100 と仮定してよい． m は，点の組の個数であり，1 ≤ m ≤ 10 と仮定してよい． 続く n 行のそれぞれは，空白文字 1 個で区切られた 3 個の整数からなる． (Cx_i, Cy_i) と r_i は， i 番目の円の中心の位置と半径を表す． 引き続く m 行のそれぞれは，空白文字 1 個で区切られた 4 個の整数からなる． この 4 個の整数は 2 つの異なる点 P_j = (Px_j, Py_j) と Q_j =(Qx_j, Qy_j) の座標を与える． この 2 点 P_j と Q_j が j 番目の点の組である． 0 ≤ Cx_i ≤ 10000, 0 ≤ Cy_i ≤ 10000, 1 ≤ r_i ≤ 1000, 0 ≤ Px_j ≤ 10000, 0 ≤ Py_j ≤ 10000, 0 ≤ Qx_j ≤ 10000, 0 ≤ Qy_j ≤ 10000 と仮定してよい． また，P_j および Q_j は，どの円の円周上にも存在することはない．

入力の終わりは，空白文字 1 個で区切られた 2 個のゼロからなる行で表される．

なお，図 G-1 は，後に示す Sample Input 中の最初のデータセットにおける 円と点の配置を表している． 図 G-2 は，Sample Input 中の残りのデータセットにおける配置を表している．

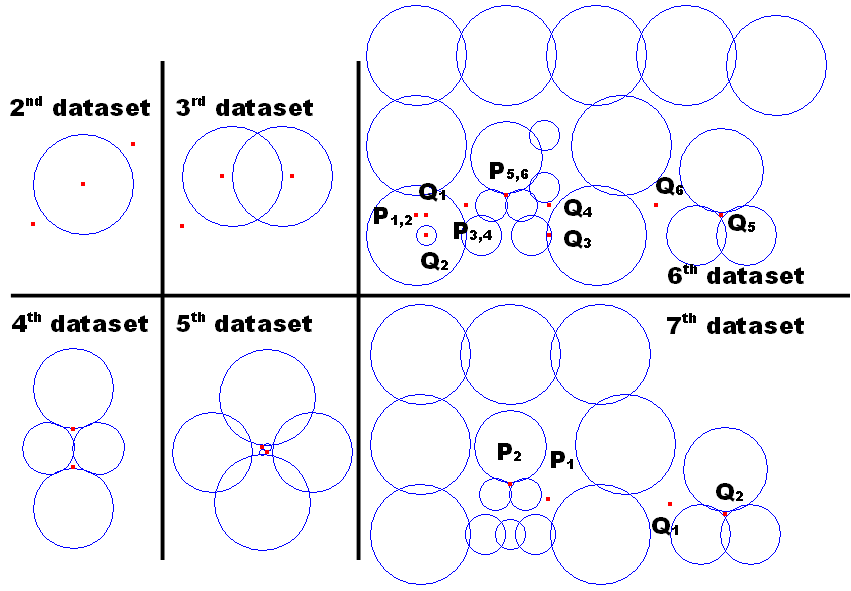
図 G-2: 円および点の配置例

Output

各データセットに対して， m 個の結果を，空白文字 1 個で区切って，1 行に出力せよ． ただし，j 番目の結果には P_j と Q_j を 結ぶパスが存在する場合は "YES" を，存在しない場合は "NO" を出力すること．

Sample Input

5 3
0 0 1000
1399 1331 931
0 1331 500
1398 0 400
2000 360 340
450 950 1600 380
450 950 1399 1331
450 950 450 2000
1 2
50 50 50
0 10 100 90
0 10 50 50
2 2
50 50 50
100 50 50
40 50 110 50
40 50 0 0
4 1
25 100 26
75 100 26
50 40 40
50 160 40
50 81 50 119
6 1
100 50 40
0 50 40
50 0 48
50 50 3
55 55 4
55 105 48
50 55 55 50
20 6
270 180 50
360 170 50
0 0 50
10 0 10
0 90 50
0 180 50
90 180 50
180 180 50
205 90 50
180 0 50
65 0 20
75 30 16
90 78 36
105 30 16
115 0 20
128 48 15
128 100 15
280 0 30
330 0 30
305 65 42
0 20 10 20
0 20 10 0
50 30 133 0
50 30 133 30
90 40 305 20
90 40 240 30
16 2
0 0 50
0 90 50
0 180 50
90 180 50
180 180 50
205 90 50
180 0 50
65 0 20
115 0 20
90 0 15
280 0 30
330 0 30
305 65 42
75 40 16
90 88 36
105 40 16
128 35 250 30
90 50 305 20
0 0

Output for the Sample Input

YES NO NO
YES NO
NO NO
NO
YES
YES NO NO YES NO NO
NO NO

---