Problem E: Pipeline Scheduling
An arithmetic pipeline is designed to process more than one task simultaneously in an overlapping manner. It includes function units and data paths among them. Tasks are processed by pipelining: at each clock, one or more units are dedicated to a task and the output produced for the task at the clock is cascading to the units that are responsible for the next stage; since each unit may work in parallel with the others at any clock, more than one task may be being processed at a time by a single pipeline.
In this problem, a pipeline may have a feedback structure, that is, data paths among function units may have directed loops as shown in the next figure.

Since an arithmetic pipeline in this problem is designed as special purpose dedicated hardware, we assume that it accepts just a single sort of task. Therefore, the timing information of a pipeline is fully described by a simple table called a reservation table, which specifies the function units that are busy at each clock when a task is processed without overlapping execution.
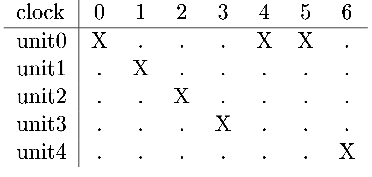
In reservation tables, 'X' means "the function unit is busy at that clock" and '.' means "the function unit is not busy at that clock." In this case, once a task enters the pipeline, it is processed by unit0 at the first clock, by unit1 at the second clock, and so on. It takes seven clock cycles to perform a task.
Notice that no special hardware is provided to avoid simultaneous use of the same function unit.
Therefore, a task must not be started if it would conflict with any tasks being processed. For instance, with the above reservation table, if two tasks, say task 0 and task 1, were started at clock 0 and clock 1, respectively, a conflict would occur on unit0 at clock 5. This means that you should not start two tasks with single cycle interval. This invalid schedule is depicted in the following process table, which is obtained by overlapping two copies of the reservation table with one being shifted to the right by 1 clock.
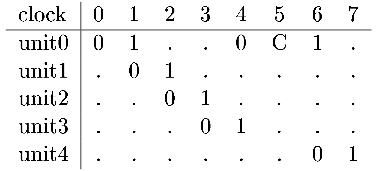
('0's and '1's in this table except those in the first row represent tasks 0 and 1, respectively, and 'C' means the conflict.)
Your job is to write a program that reports the minimum number of clock cycles in which the given pipeline can process 10 tasks.
Input
The input consists of multiple data sets, each representing the reservation table of a pipeline. A data set is given in the following format.
n x0,0 x0,1 ... x0,n-1 x1,0 x1,1 ... x1,n-1 x2,0 x2,1 ... x2,n-1 x3,0 x3,1 ... x3,n-1 x4,0 x4,1 ... x4,n-1
The integer n (< 20) in the first line is the width of the reservation table, or the number of clock cycles that is necessary to perform a single task. The second line represents the usage of unit0, the third line unit1, and so on. xi,j is either 'X' or '.'. The former means reserved and the latter free. There are no spaces in any input line. For simplicity, we only consider those pipelines that consist of 5 function units. The end of the input is indicated by a data set with 0 as the value of n.
Output
For each data set, your program should output a line containing an integer number that is the minimum number of clock cycles in which the given pipeline can process 10 tasks.
Sample Input
7 X...XX. .X..... ..X.... ...X... ......X 0
Output for the Sample Input
34
In this sample case, it takes 41 clock cycles process 10 tasks if each task is started as early as possible under the condition that it never conflicts with any previous tasks being processed.

(The digits in the table except those in the clock row represent the task number.)
However, it takes only 34 clock cycles if each task is started at every third clock.

(The digits in the table except those in the clock row represent the task number.)
This is the best possible schedule and therefore your program should report 34 in this case.