Problem F: Numoeba
A scientist discovered a strange variation of amoeba. The scientist named it numoeba. A numoeba, though it looks like an amoeba, is actually a community of cells, which always forms a tree.
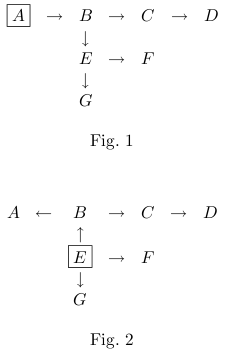
The scientist called the cell leader that is at the root position of the tree. For example, in Fig. 1, the leader is A. In a numoeba, its leader may change time to time. For example, if E gets new leadership, the tree in Fig. 1 becomes one in Fig. 2. We will use the terms root, leaf, parent, child and subtree for a numoeba as defined in the graph theory.
Numoeba changes its physical structure at every biological clock by cell division and cell death. The leader may change depending on this physical change.
The most astonishing fact about the numoeba cell is that it contains an organic unit called numbosome, which represents an odd integer within the range from 1 to 12,345,677. At every biological clock, the value of a numbosome changes from n to a new value as follows:
- The maximum odd factor of 3n + 1 is calculated. This value can be obtained from 3n + 1 by repeating division by 2 while even.
- If the resulting integer is greater than 12,345,678, then it is subtracted by 12,345,678.
For example, if the numbosome value of a cell is 13, 13 × 3 + 1 = 40 is divided by 23 = 8 and a new numbosome value 5 is obtained. If the numbosome value of a cell is 11,111,111, it changes to 4,320,989, instead of 16,666,667. If 3n + 1 is a power of 2, yielding 1 as the result, it signifies the death of the cell as will be described below.
At every biological clock, the next numbosome value of every cell is calculated and the fate of the cell and thereby the fate of numoeba is determined according to the following steps.
- A cell that is a leaf and increases its numbosome value is designated as a candidate leaf.
A cell dies if its numbosome value becomes 1. If the dying cell is the leader of the numoeba, the numoeba dies as a whole. Otherwise, all the cells in the subtree from the dying cell (including itself) die. However, there is an exceptional case where the cells in the subtree do not necessarily die; if there is only one child cell of the dying non-leader cell, the child cell will replace the dying cell. Thus, a straight chain simply shrinks if its non-leader constituent dies.
For example, consider a numoeba with the leader A below.
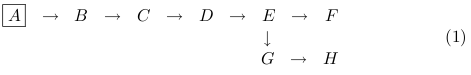
If the leader A dies in (1), the numoeba dies.
If the cell D dies in (1), (1) will be as follows.
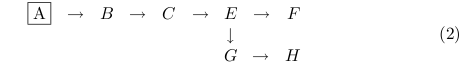
And, if the cell E dies in (1), (1) will be as follows.
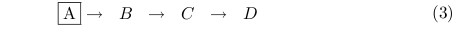
Note that this procedure is executed sequentially, top-down from the root of the numoeba to leaves. If the cells E and F will die in (1), the death of F is not detected at the time the procedure examines the cell E. The numoeba, therefore, becomes (3). One should not consider in such a way that the death of F makes G the only child of E, and, therefore, G will replace the dying E. - If a candidate leaf survives with the numbosome value of n, it spawns a cell as its child, thereby a new leaf, whose numbosome value is the least odd integer greater than or equal to (n + 1)/2. We call the child leaf bonus.
- Finally, a new leader of the numoeba is selected, who has a unique maximum numbosome value among all the constituent cells. The tree structure of the numoeba is changed so that the new leader is its root, like what is shown in Fig. 1 and Fig. 2. Note that the parent-child relationship of some cells may be reversed by this leader change. When a new leader of a unique maximum numbosome value, say m, is selected (it may be the same cell as the previous leader), it spawns a cell as its child with the numbosome whose value is the greatest odd integer less than or equal to (m + 1)/2. We call the child leader bonus. If there is more than one cell of the same maximum numbosome value, however, the leader does not change for the next period, and there is no leader bonus.
The following illustrates the growth and death of a numoeba starting from a single cell seed with the numbosome value 15, which plays both roles of the leader and a leaf at the start. In the figure, a cell is nicknamed with its numbosome value. Note that the order of the children of a parent is irrelevant.


The numoeba continues changing its structure, and at clock 104, it looks as follows.
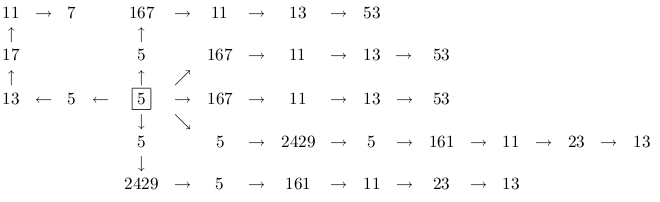
Here, two ambitious 2429's could not become the leader. The leader 5 will die without promoting these talented cells at the next clock. This alludes the fragility of a big organization.
And, the numoeba dies at clock 105.
Your job is to write a program that outputs statistics about the life of numoebae that start from a single cell seed at clock zero.
Input
A sequence of odd integers, each in a line. Each odd integer ki (3 ≤ ki ≤ 9,999) indicates the initial numbosome value of the starting cell. This sequence is terminated by a zero.
Output
A sequence of pairs of integers:an integer that represents the numoeba's life time and an integer that represents the maximum number of constituent cells in its life. These two integers should be separated by a space character, and each pair should be followed immediately by a newline. Here, the lifetime means the clock when the numoeba dies.
You can use the fact that the life time is less than 500, and that the number of cells does not exceed 500 in any time, for any seed value given in the input. You might guess that the program would consume a lot of memory. It is true in general. But, don't mind. Referees will use a test data set consisting of no more than 10 starting values, and, starting from any of the those values, the total numbers of cells spawned during the lifetime will not exceed 5000.
Sample Input
3 5 7 15 655 2711 6395 7195 8465 0
Output for the Sample Input
2 3 1 1 9 11 105 65 398 332 415 332 430 332 428 332 190 421