Problem J: Zigzag

Given several points on a plane, let’s try to solve a puzzle connecting them with a zigzag line. The puzzle is to find the zigzag line that passes through all the given points with the minimum number of turns. Moreover, when there are several zigzag lines with the minimum number of turns, the shortest one among them should be found.

For example, consider nine points given in Figure 1.

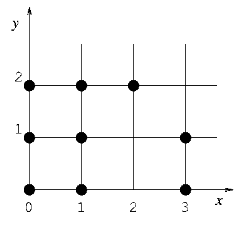
Figure 1: Given nine points

A zigzag line is composed of several straight line segments. Here, the rule requests that each line segment should pass through two or more given points.

A zigzag line may turn at some of the given points or anywhere else. There may be some given points passed more than once.

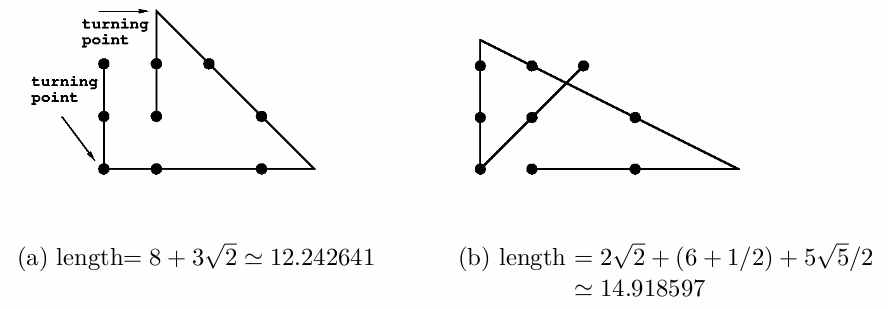
Figure 2: Zigzag lines with three turning points.

Two zigzag lines with three turning points are depicted in Figure 2 (a) and (b) for the same set of given points shown in Figure 1. The length of the zigzag line in Figure 2 (a) is shorter than that in Figure 2 (b). In fact, the length of the zigzag line in Figure 2 (a) is the shortest so that it is the solution for the nine points given in Figure 1.

Another zigzag line with four turning points is depicted in Figure 3. Its length is shorter than those in Figure 2, however, the number of turning points is greater than those in Figure 2, and thus, it is not the solution.

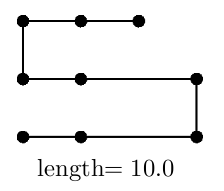
Figure 3: Zigzag line with four turning points.

There are two zigzag lines that passes another set of given points depicted in Figure 4 (a) and (b).

Both have the same number of turning points, and the line in (a) is longer than that in (b). However, the solution is (a), because one of the segments of the zigzag line in (b) passes only one given point, violating the rule.

Figure 4: Zigzag line with two turning points (a), and not a zigzag line concerned (b).

Your job is to write a program that solves this puzzle.

Input

The input consists of multiple datasets, followed by a line containing one zero. Each dataset has the following format.

n
x1 y1
   .
   .
   .
xn yn

Every input item in a dataset is a non-negative integer. Items in a line are separated by a single space.

n is the number of the given points. x_k and y_k (k = 1, . . . , n) indicate the position of the k-th point. The order of the points is meaningless. You can assume that 2 ≤ n ≤ 10, 0 ≤ x_k ≤ 10, and 0 ≤ y_k ≤ 10.

Output

For each dataset, the minimum number of turning points and the length of the shortest zigzag line with that number of turning points should be printed, separated by a space in a line. The length should be in a decimal fraction with an error less than 0.0001 (= 1.0 × 10^-4 ).

You may assume that the minimum number of turning points is at most four, that is, the number of line segments is at most five.

The example solutions for the first four datasets in the sample input are depicted in Figure 5 and 6.

Sample Input

2
0 0
10 9
4
0 0
3 1
0 3
3 3
10
2 2
4 2
6 2
2 4
4 4
6 4
2 6
4 6
6 6
3 3
10
0 0
2 0
4 0
0 2
2 2
4 2
0 4
2 4
4 4
6 8
9
0 0
1 0
3 0
0 1
1 1
3 1
0 2
1 2
2 2
10
0 0
1 0
0 1
1 1
9 9
9 10
10 9
10 10
0 2
10 8
10
0 0
0 10
2 0
2 1
2 7
2 10
5 1
6 7
9 2
10 9
0

Output for the Sample Input

0 13.45362405
1 18.48683298
3 24.14213562
4 24.94813673
3 12.24264069
3 60.78289622
3 502.7804353

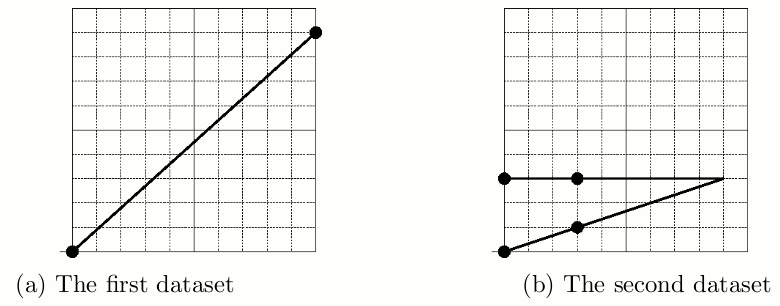
Figure 5: Example solutions for the first and the second datasets in the sample inputs.

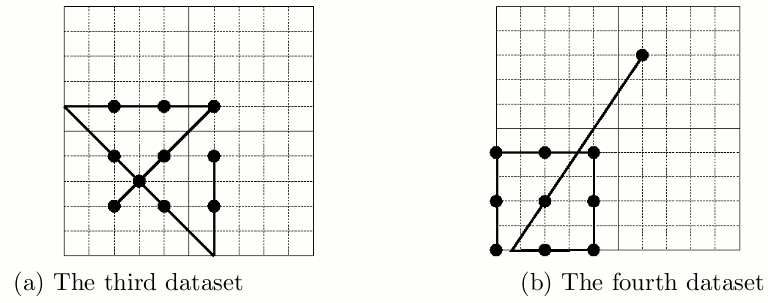
Figure 6: Example solutions for the third and the fourth datasets in the sample inputs.

---