Problem G: Malfatti Circles
The configuration of three circles packed inside a triangle such that each circle is tangent to the other two circles and to two of the edges of the triangle has been studied by many mathematicians for more than two centuries. Existence and uniqueness of such circles for an arbitrary triangle are easy to prove. Many methods of numerical calculation or geometric construction of such circles from an arbitrarily given triangle have been discovered. Today, such circles are called the Malfatti circles.
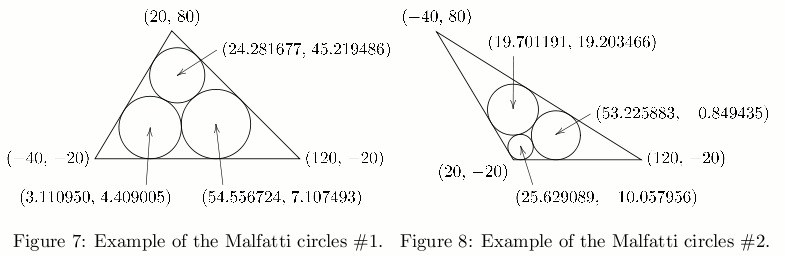
Figure 7 illustrates an example. The Malfatti circles of the triangle with the vertices (20, 80), (-40, -20) and (120, -20) are approximately
- the circle with the center (24.281677, 45.219486) and the radius 21.565935,
- the circle with the center (3.110950, 4.409005) and the radius 24.409005, and
- the circle with the center (54.556724, 7.107493) and the radius 27.107493.
Figure 8 illustrates another example. The Malfatti circles of the triangle with the vertices (20, -20), (120, -20) and (-40, 80) are approximately
- the circle with the center (25.629089, −10.057956) and the radius 9.942044,
- the circle with the center (53.225883, −0.849435) and the radius 19.150565, and
- the circle with the center (19.701191, 19.203466) and the radius 19.913790.
Your mission is to write a program to calculate the radii of the Malfatti circles of the given triangles.
Input
The input is a sequence of datasets. A dataset is a line containing six integers x1, y1 , x2 , y2, x3 and y3 in this order, separated by a space. The coordinates of the vertices of the given triangle are (x1 , y1 ), (x2 , y2 ) and (x3 , y3 ), respectively. You can assume that the vertices form a triangle counterclockwise. You can also assume that the following two conditions hold.
- All of the coordinate values are greater than −1000 and less than 1000.
- None of the Malfatti circles of the triangle has a radius less than 0.1.
The end of the input is indicated by a line containing six zeros separated by a space.
Output
For each input dataset, three decimal fractions r1 , r2 and r3 should be printed in a line in this order separated by a space. The radii of the Malfatti circles nearest to the vertices with the coordinates (x1 , y1 ), (x2 , y2 ) and (x3 , y3 ) should be r1 , r2 and r3 , respectively.
None of the output values may have an error greater than 0.0001. No extra character should appear in the output.
Sample Input
20 80 -40 -20 120 -20 20 -20 120 -20 -40 80 0 0 1 0 0 1 0 0 999 1 -999 1 897 -916 847 -972 890 -925 999 999 -999 -998 -998 -999 -999 -999 999 -999 0 731 -999 -999 999 -464 -464 999 979 -436 -955 -337 157 -439 0 0 0 0 0 0
Output for the Sample Input
21.565935 24.409005 27.107493 9.942044 19.150565 19.913790 0.148847 0.207107 0.207107 0.125125 0.499750 0.499750 0.373458 0.383897 0.100456 0.706768 0.353509 0.353509 365.638023 365.638023 365.601038 378.524085 378.605339 378.605339 21.895803 22.052921 5.895714