Problem B: The Sorcerer's Donut
Your master went to the town for a day. You could have a relaxed day without hearing his scolding. But he ordered you to make donuts dough by the evening. Loving donuts so much, he can't live without eating tens of donuts everyday. What a chore for such a beautiful day.
But last week, you overheard a magic spell that your master was using. It was the time to try. You casted the spell on a broomstick sitting on a corner of the kitchen. With a flash of lights, the broom sprouted two arms and two legs, and became alive. You ordered him, then he brought flour from the storage, and started kneading dough. The spell worked, and how fast he kneaded it!
A few minutes later, there was a tall pile of dough on the kitchen table. That was enough for the next week. \OK, stop now." You ordered. But he didn't stop. Help! You didn't know the spell to stop him! Soon the kitchen table was filled with hundreds of pieces of dough, and he still worked as fast as he could. If you could not stop him now, you would be choked in the kitchen filled with pieces of dough.
Wait, didn't your master write his spells on his notebooks? You went to his den, and found the notebook that recorded the spell of cessation.
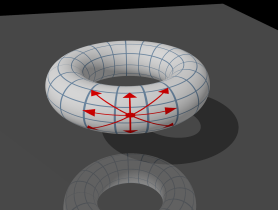
But it was not the end of the story. The spell written in the notebook is not easily read by others. He used a plastic model of a donut as a notebook for recording the spell. He split the surface of the donut-shaped model into square mesh (Figure B.1), and filled with the letters (Figure B.2). He hid the spell so carefully that the pattern on the surface looked meaningless. But you knew that he wrote the pattern so that the spell "appears" more than once (see the next paragraph for the precise conditions). The spell was not necessarily written in the left-to-right direction, but any of the 8 directions, namely left-to-right, right-to-left, top-down, bottom-up, and the 4 diagonal directions.
You should be able to find the spell as the longest string that appears more than once. Here,
a string is considered to appear more than once if there are square sequences having the string
on the donut that satisfy the following conditions.
|

|
| Figure B.1: The Sorcerer's Donut Before Filled with Letters, Showing the Mesh and 8 Possible Spell Directions | Figure B.2: The Sorcerer's Donut After Filled with Letters |
Note that a palindrome (i.e., a string that is the same whether you read it backwards or forwards) that satisfies the first condition "appears" twice.
The pattern on the donut is given as a matrix of letters as follows.
ABCD EFGH IJKL
Note that the surface of the donut has no ends; the top and bottom sides, and the left and right sides of the pattern are respectively connected. There can be square sequences longer than both the vertical and horizontal lengths of the pattern. For example, from the letter F in the above pattern, the strings in the longest non-self-overlapping sequences towards the 8 directions are as follows.
FGHE FKDEJCHIBGLA FJB FIDGJAHKBELC FEHG FALGBIHCJEDK FBJ FCLEBKHAJGDI
Please write a program that finds the magic spell before you will be choked with pieces of donuts dough.
Input
The input is a sequence of datasets. Each dataset begins with a line of two integers h and w, which denote the size of the pattern, followed by h lines of w uppercase letters from A to Z, inclusive, which denote the pattern on the donut. You may assume 3 ≤ h ≤ 10 and 3 ≤ w ≤ 20.
The end of the input is indicated by a line containing two zeros.
Output
For each dataset, output the magic spell. If there is more than one longest string of the same length, the first one in the dictionary order must be the spell. The spell is known to be at least two letters long. When no spell is found, output 0 (zero).
Sample Input
5 7 RRCABXT AABMFAB RROMJAC APTADAB YABADAO 3 13 ABCDEFGHIJKLM XMADAMIMADAMY ACEGIKMOQSUWY 3 4 DEFG ACAB HIJK 3 6 ABCDEF GHIAKL MNOPQR 10 19 JFZODYDXMZZPEYTRNCW XVGHPOKEYNZTQFZJKOD EYEHHQKHFZOVNRGOOLP QFZOIHRQMGHPNISHXOC DRGILJHSQEHHQLYTILL NCSHQMKHTZZIHRPAUJA NCCTINCLAUTFJHSZBVK LPBAUJIUMBVQYKHTZCW XMYHBVKUGNCWTLLAUID EYNDCCWLEOODXYUMBVN 0 0
Output for the Sample Input
ABRACADABRA MADAMIMADAM ABAC 0 ABCDEFGHIJKLMNOPQRSTUVWXYZHHHHHABCDEFGHIJKLMNOPQRSTUVWXYZ