Problem E: Sliding Block Puzzle

In sliding block puzzles, we repeatedly slide pieces (blocks) to open spaces within a frame to establish a goal placement of pieces.

A puzzle creator has designed a new puzzle by combining the ideas of sliding block puzzles and mazes. The puzzle is played in a rectangular frame segmented into unit squares. Some squares are pre-occupied by obstacles. There are a number of pieces placed in the frame, one 2 × 2 king piece and some number of 1 × 1 pawn pieces. Exactly two 1 × 1 squares are left open. If a pawn piece is adjacent to an open square, we can slide the piece there. If a whole edge of the king piece is adjacent to two open squares, we can slide the king piece. We cannot move the obstacles. Starting from a given initial placement, the objective of the puzzle is to move the king piece to the upper-left corner of the frame.

The following figure illustrates the initial placement of the fourth dataset of the sample input.

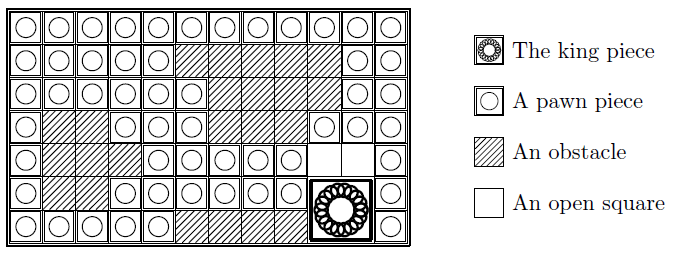
Figure E.1: The fourth dataset of the sample input.

Your task is to write a program that computes the minimum number of moves to solve the puzzle from a given placement of pieces. Here, one move means sliding either king or pawn piece to an adjacent position.

Input

The input is a sequence of datasets. The first line of a dataset consists of two integers H and W separated by a space, where H and W are the height and the width of the frame. The following H lines, each consisting of W characters, denote the initial placement of pieces. In those H lines, 'X', 'o', '*', and '.' denote a part of the king piece, a pawn piece, an obstacle, and an open square, respectively. There are no other characters in those H lines. You may assume that 3 ≤ H ≤ 50 and 3 ≤ W ≤ 50.

A line containing two zeros separated by a space indicates the end of the input.

Output

For each dataset, output a line containing the minimum number of moves required to move the king piece to the upper-left corner. If there is no way to do so, output -1.

Sample Input

3 3
oo.
oXX
.XX
3 3
XXo
XX.
o.o
3 5
.o*XX
oooXX
oooo.
7 12
oooooooooooo
ooooo*****oo
oooooo****oo
o**ooo***ooo
o***ooooo..o
o**ooooooXXo
ooooo****XXo
5 30
oooooooooooooooooooooooooooooo
oooooooooooooooooooooooooooooo
o***************************oo
XX.ooooooooooooooooooooooooooo
XX.ooooooooooooooooooooooooooo
0 0

Output for the Sample Input

11
0
-1
382
6807

---