Problem I: Beautiful Spacing

Text is a sequence of words, and a word consists of characters. Your task is to put words into a grid with W columns and sufficiently many lines. For the beauty of the layout, the following conditions have to be satisfied.

1. The words in the text must be placed keeping their original order. The following figures show correct and incorrect layout examples for a 4 word text "This is a pen" into 11 columns.
   
   

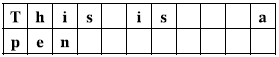
   Figure I.1: A good layout.	Figure I.2: BAD | Do not reorder words.

   
   
2. Between two words adjacent in the same line, you must place at least one space character. You sometimes have to put more than one space in order to meet other conditions.
   
   
   

   Figure I.3: BAD | Words must be separated by spaces.

   
   
3. A word must occupy the same number of consecutive columns as the number of characters in it. You cannot break a single word into two or more by breaking it into lines or by inserting spaces.
   
   
   

   Figure I.4: BAD | Characters in a single word must be contiguous.

   
   
4. The text must be justified to the both sides. That is, the first word of a line must startfrom the first column of the line, and except the last line, the last word of a line must end at the last column.
   
   
   

   Figure I.5: BAD | Lines must be justied to both the left and the right sides.

The text is the most beautifully laid out when there is no unnecessarily long spaces. For instance, the layout in Figure I.6 has at most 2 contiguous spaces, which is more beautiful than that in Figure I.1, having 3 contiguous spaces. Given an input text and the number of columns, please find a layout such that the length of the longest contiguous spaces between words is minimum.

Figure I.6: A good and the most beautiful layout.

Input

The input consists of multiple datasets, each in the following format.

    W N
    x₁ x₂ ... x_N

W, N, and x_i are all integers. W is the number of columns (3 ≤ W ≤ 80,000). N is the number of words (2 ≤ N ≤ 50,000). x_i is the number of characters in the i-th word (1 ≤ x_i ≤ (W−1)/2 ). Note that the upper bound on x_i assures that there always exists a layout satisfying the conditions.

The last dataset is followed by a line containing two zeros.

Output

For each dataset, print the smallest possible number of the longest contiguous spaces between words.

Sample Input

11 4
4 2 1 3
5 7
1 1 1 2 2 1 2
11 7
3 1 3 1 3 3 4
100 3
30 30 39
30 3
2 5 3
0 0

Output for the Sample Input

2
1
2
40
1

---