Problem K: $L_{\infty}$ Jumps

Given two points $(p, q)$ and $(p', q')$ in the XY-plane, the $L_{\infty}$ distance between them is defined as $max(|p − p'|, |q − q'|)$. In this problem, you are given four integers $n$, $d$, $s$, $t$. Suppose that you are initially standing at point $(0, 0)$ and you need to move to point $(s, t)$. For this purpose, you perform jumps exactly $n$ times. In each jump, you must move exactly $d$ in the $L_{\infty}$ distance measure. In addition, the point you reach by a jump must be a lattice point in the XY-plane. That is, when you are standing at point $(p, q)$, you can move to a new point $(p', q')$ by a single jump if $p'$ and $q'$ are integers and $max(|p − p'|, |q − q'|) = d$ holds.

Note that you cannot stop jumping even if you reach the destination point $(s, t)$ before you perform the jumps $n$ times.

To make the problem more interesting, suppose that some cost occurs for each jump. You are given $2n$ additional integers $x_1$, $y_1$, $x_2$, $y_2$, . . . , $x_n$, $y_n$ such that $max(|x_i|, |y_i|) = d$ holds for each $1 \leq i \leq n$. The cost of the $i$-th (1-indexed) jump is defined as follows: Let $(p, q)$ be a point at which you are standing before the $i$-th jump. Consider a set of lattice points that you can jump to. Note that this set consists of all the lattice points on the edge of a certain square. We assign integer 1 to point $(p + x_i, q + y_i)$. Then, we assign integers $2, 3, . . . , 8d$ to the remaining points in the set in the counter-clockwise order. (Here, assume that the right direction is positive in the $x$-axis and the upper direction is positive in the $y$-axis.) These integers represent the costs when you perform a jump to these points.

For example, Figure K.1 illustrates the points reachable by your $i$-th jump when $d = 2$ and you are at $(3, 1)$. The numbers represent the costs for $x_i = −1$ and $y_i = −2$.

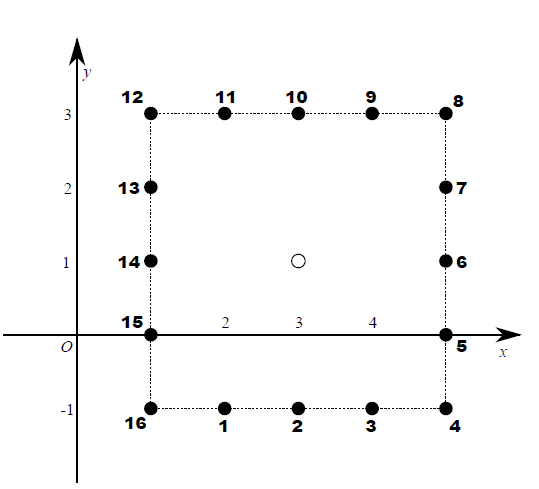
Figure K.1. Reachable points and their costs

Compute and output the minimum required sum of the costs for the objective.

Input

The input consists of a single test case.

$n$ $d$ $s$ $t$
$x_1$ $y_1$
$x_2$ $y_2$
.
.
.
$x_n$ $y_n$

The first line contains four integers. $n$ ($1 \leq n \leq 40$) is the number of jumps to perform. $d$ ($1 \leq d \leq 10^{10}$) is the $L_{\infty}$ distance which you must move by a single jump. $s$ and $t$ ($|s|, |t| \leq nd$) are the $x$ and $y$ coordinates of the destination point. It is guaranteed that there is at least one way to reach the destination point by performing $n$ jumps.

Each of the following $n$ lines contains two integers, $x_i$ and $y_i$ with $max(|x_i|, |y_i|) = d$.

Output

Output the minimum required cost to reach the destination point.

Sample Input 1

3 2 4 0
2 2
-2 -2
-2 2

Sample Output 1

15

Sample Input 2

4 1 2 -2
1 -1
1 0
1 1
-1 0

Sample Output 2

10

Sample Input 3

6 5 0 2
5 2
-5 2
5 0
-3 5
-5 4
5 5

Sample Output 3

24

Sample Input 4

5 91 -218 -351
91 91
91 91
91 91
91 91
91 91

Sample Output 4

1958

Sample Input 5

1 10000000000 -10000000000 -2527532346
8198855077 10000000000

Sample Output 5

30726387424

---