Problem C Sibling Rivalry

You are playing a game with your elder brother.

First, a number of circles and arrows connecting some pairs of the circles are drawn on the ground. Two of the circles are marked as the start circle and the goal circle.

At the start of the game, you are on the start circle. In each turn of the game, your brother tells you a number, and you have to take that number of steps. At each step, you choose one of the arrows outgoing from the circle you are on, and move to the circle the arrow is heading to. You can visit the same circle or use the same arrow any number of times.

Your aim is to stop on the goal circle after the fewest possible turns, while your brother's aim is to prevent it as long as possible. Note that, in each single turn, you must take the exact number of steps your brother tells you. Even when you visit the goal circle during a turn, you have to leave it if more steps are to be taken.

If you reach a circle with no outgoing arrows before completing all the steps, then you lose the game. You also have to note that, your brother may be able to repeat turns forever, not allowing you to stop after any of them.

Your brother, mean but not too selfish, thought that being allowed to choose arbitrary numbers is not fair. So, he decided to declare three numbers at the start of the game and to use only those numbers.

Your task now is, given the configuration of circles and arrows, and the three numbers declared, to compute the smallest possible number of turns within which you can always finish the game, no matter how your brother chooses the numbers.

Input

The input consists of a single test case, formatted as follows.

$n$ $m$ $a$ $b$ $c$
$u_1$ $v_1$
...
$u_m$ $v_m$

All numbers in a test case are integers. $n$ is the number of circles $(2 \leq n \leq 50)$. Circles are numbered 1 through $n$. The start and goal circles are numbered 1 and $n$, respectively. $m$ is the number of arrows $(0 \leq m \leq n(n - 1))$. $a$, $b$, and $c$ are the three numbers your brother declared $(1 \leq a, b, c \leq 100)$. The pair, $u_i$ and $v_i$, means that there is an arrow from the circle $u_i$ to the circle $v_i$. It is ensured that $u_i \ne v_i$ for all $i$, and $u_i \ne u_j$ or $v_i \ne v_j$ if $i \ne j$.

Output

Print the smallest possible number of turns within which you can always finish the game. Print IMPOSSIBLE if your brother can prevent you from reaching the goal, by either making you repeat the turns forever or leading you to a circle without outgoing arrows.

Sample Input 1

3 3 1 2 4
1 2
2 3
3 1

Sample Output 1

IMPOSSIBLE

Sample Input 2

8 12 1 2 3
1 2
2 3
1 4
2 4
3 4
1 5
5 8
4 6
6 7
4 8
6 8
7 8

Sample Output 2

2

For Sample Input 1, your brother may choose 1 first, then 2, and repeat these forever. Then you can never finish.

For Sample Input 2 (Figure C.1), if your brother chooses 2 or 3, you can finish with a single turn. If he chooses 1, you will have three options.

• Move to the circle 5. This is a bad idea: Your brother may then choose 2 or 3 and make you lose.
• Move to the circle 4. This is the best choice: From the circle 4, no matter any of 1, 2, or 3 your brother chooses in the next turn, you can finish immediately.
• Move to the circle 2. This is not optimal for you. If your brother chooses 1 in the next turn, you cannot finish yet. It will take three or more turns in total.

In summary, no matter how your brother acts, you can finish within two turns. Thus the answer is 2.

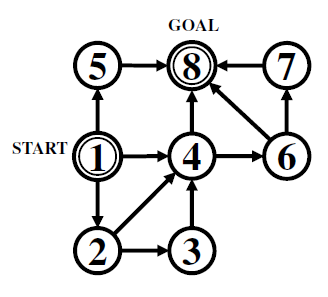
Figure C.1. Sample Input 2

---