Problem D Making Perimeter of the Convex Hull Shortest
The convex hull of a set of three or more planar points is, when not all of them are on one line, the convex polygon with the smallest area that has all the points of the set on its boundary or in its inside. Your task is, given positions of the points of a set, to find how much shorter the perimeter of the convex hull can be made by excluding two points from the set.
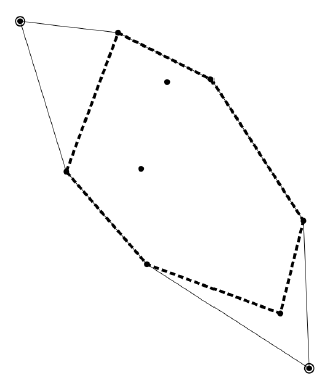
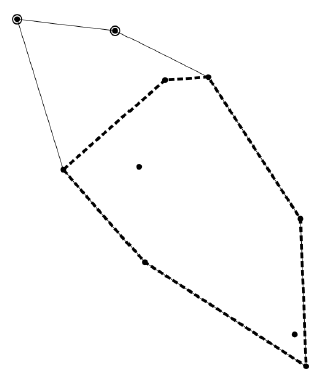
The figures below correspond to the three cases given as Sample Input 1 to 3. Encircled points are excluded to make the shortest convex hull depicted as thick dashed lines.
 |
 |
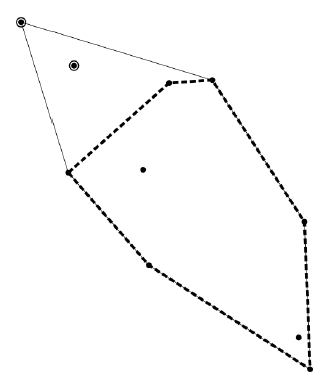 |
| Sample Input 1 | Sample Input 2 | Sample Input 3 |
Input
The input consists of a single test case in the following format.
$n$ $x_1$ $y_1$ ... $x_n$ $y_n$
Here, $n$ is the number of points in the set satisfying $5 \leq n \leq 10^5$. For each $i$, ($x_i, y_i$) gives the coordinates of the position of the $i$-th point in the set. $x_i$ and $y_i$ are integers between $-10^6$ and $10^6$, inclusive. All the points in the set are distinct, that is, $x_j \ne x_k$ or $y_j \ne y_k$ holds when $j \ne k$. It is guaranteed that no single line goes through $n - 2$ or more points in the set.
Output
Output the difference of the perimeter of the convex hull of the original set and the shortest of the perimeters of the convex hulls of the subsets with two points excluded from the original set. The output should not have an error greater than $10^{-4}$.
Sample Input 1
10 -53 62 -19 58 -11 11 -9 -22 45 -7 37 -39 47 -58 -2 41 -37 10 13 42
Sample Output 1
72.96316928
Sample Input 2
10 -53 62 -19 58 -11 11 -9 -22 45 -7 43 -47 47 -58 -2 41 -37 10 13 42
Sample Output 2
62.62947992
Sample Input 3
10 -53 62 -35 47 -11 11 -9 -22 45 -7 43 -47 47 -58 -2 41 -37 10 13 42
Sample Output 3
61.58166534