Emergency Evacuation
The Japanese government plans to increase the number of inbound tourists to forty million in the year 2020, and sixty million in 2030. Not only increasing touristic appeal but also developing tourism infrastructure further is indispensable to accomplish such numbers.
One possible enhancement on transport is providing cars extremely long and/or wide, carrying many passengers at a time. Too large a car, however, may require too long to evacuate all passengers in an emergency. You are requested to help estimating the time required.
The car is assumed to have the following seat arrangement.
- A center aisle goes straight through the car, directly connecting to the emergency exit door at the rear center of the car.
- The rows of the same number of passenger seats are on both sides of the aisle.
A rough estimation requested is based on a simple step-wise model. All passengers are initially on a distinct seat, and they can make one of the following moves in each step.
- Passengers on a seat can move to an adjacent seat toward the aisle. Passengers on a seat adjacent to the aisle can move sideways directly to the aisle.
- Passengers on the aisle can move backward by one row of seats. If the passenger is in front of the emergency exit, that is, by the rear-most seat rows, he/she can get off the car.
The seat or the aisle position to move to must be empty; either no other passenger is there before the step, or the passenger there empties the seat by moving to another position in the same step. When two or more passengers satisfy the condition for the same position, only one of them can move, keeping the others wait in their original positions.
The leftmost figure of Figure C.1 depicts the seat arrangement of a small car given in Sample Input 1. The car have five rows of seats, two seats each on both sides of the aisle, totaling twenty. The initial positions of seven passengers on board are also shown.
The two other figures of Figure C.1 show possible positions of passengers after the first and the second steps. Passenger movements are indicated by fat arrows. Note that, two of the passengers in the front seat had to wait for a vacancy in the first step, and one in the second row had to wait in the next step.
Your task is to write a program that gives the smallest possible number of steps for all the passengers to get off the car, given the seat arrangement and passengers' initial positions.
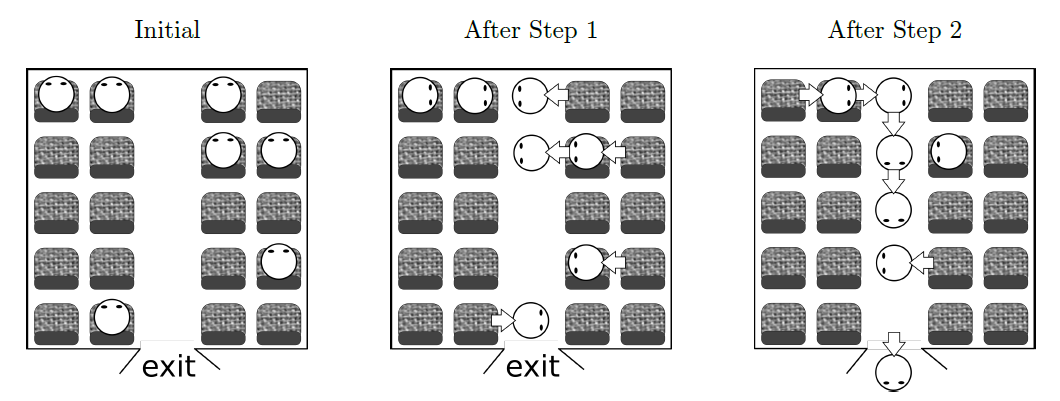
Figure C.1
Input
The input consists of a single test case of the following format.
$r$ $s$ $p$ $i_1$ $j_1$ ... $i_p$ $j_p$
Here, $r$ is the number of passenger seat rows, $s$ is the number of seats on each side of the aisle, and $p$ is the number of passengers. They are integers satisfying $1 \leq r \leq 500$, $1 \leq s \leq 500$, and $1 \leq p \leq 2rs$.
The following $p$ lines give initial seat positions of the passengers. The $k$-th line with $i_k$ and $j_k$ means that the $k$-th passenger's seat is in the $i_k$-th seat row and it is the $j_k$-th seat on that row. Here, rows and seats are counted from front to rear and left to right, both starting from one. They satisfy $1 \leq i_k \leq r$ and $1 \leq j_k \leq 2s$. Passengers are on distinct seats, that is, $i_k \ne= i_l$ or $j_k \ne j_l$ holds if $k \ne l$.
Output
The output should be one line containing a single integer, the minimum number of steps required for all the passengers to get off the car.
Sample Input 1
5 2 7 1 1 1 2 1 3 2 3 2 4 4 4 5 2
Sample Output 1
9
Sample Input 2
500 500 16 1 1 1 2 1 999 1 1000 2 1 2 2 2 999 2 1000 3 1 3 2 3 999 3 1000 499 500 499 501 499 999 499 1000
Sample Output 2
1008