Planarian Regeneration
Problem
皆さん、「プラナリア」って知っていますか?
プラナリアとは、日本では川の上流の石や枯葉などの裏に張り付いて生息している水生生物です。
プラナリアの最も優れた能力はその「再生能力」です。プラナリアの再生能力は著しく、例えば、三等分するとそれぞれが再生し、数週間後には元の完全な状態のプラナリアが3匹できあがります。
この度、会津の山奥の上流にて発見された新種のプラナリアの姿は長方形をしていて、プラナリアはある法則により再生します。 このとき、プラナリアは下の図のように配置し、2つの手段でプラナリアの切断実験を行います。
まず1つ目の手段として、垂直方向に切ることを考えます。一度の切断では、すべての断片を水平方向の長さが(断片の頭に近い部分):(断片の頭に遠い部分)=m :n になるように切断します。この動作をx 回繰り返します。
次に2つ目の手段として、水平方向に切ることを考えます。一度の切断では、すべての断片を垂直方向の長さが(断片の右端に近い部分):(断片の左端に近い部分)=k :l に切断します。この動作をy 回繰り返します。これらの切断によって断片が移動することはありません。
数週間後に、各断片が元の完全なプラナリアの状態に再生している確率は以下の式により求まります。

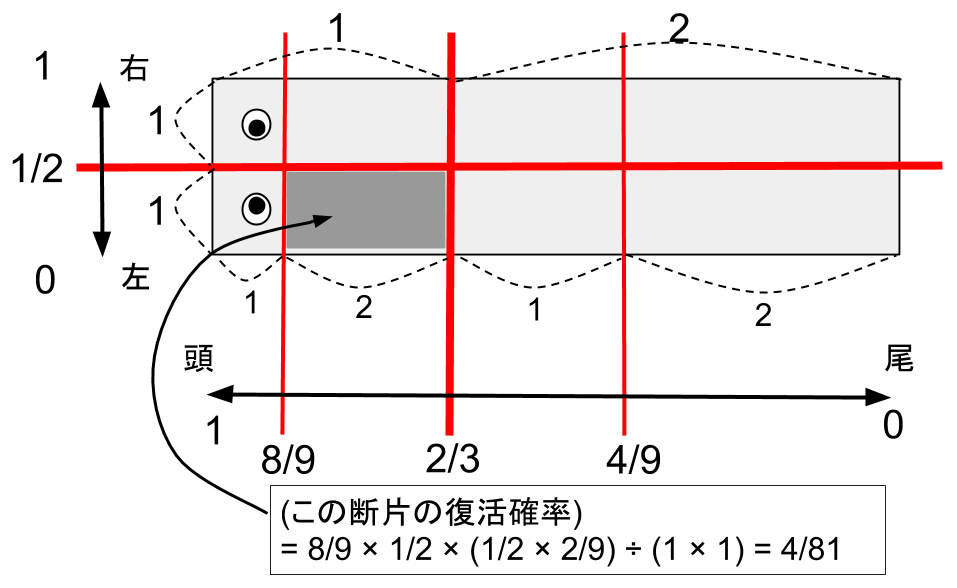
上の図は、垂直方向に1:2で2回、水平方向に1:1で1回切断した状態です。
以上の操作で切断した時の、数週間後に元の姿に再生しているプラナリアの数の期待値を求めてください。元のプラナリアの垂直方向の長さと水平方向の長さはともに1とします。
Input
m n x k l y
入力では、6つの整数m , n , x , k , l , y が上記の入力フォーマットで与えられます。
これら6つの整数は問題文中のものと対応しており、水平方向にm :n で切断する動作をx 回、垂直方向にk :l で切断する動作をy 回繰り返します。
1 ≤ m , n , k , l ≤ 100、 0 ≤ x , y ≤ 40 であり、 m , n と l , k はそれぞれ互いに素です。
Output
一行に数週間後に元の姿に再生しているプラナリアの数の期待値を出力してください。
出力は 10-6 以下の誤差ならば許容されます。
Sample Input 1
1 1 1 1 1 1
Sample Output 1
0.562500
Sample Input 2
1 2 2 1 1 1
Sample Output 2
0.490741
Sample Input 3
1 2 0 3 4 0
Sample Output 3
1.000000
Notes
この問題では、doubleよりも精度の高い浮動小数を使用することを推奨します。