Problem D: Cheat Case
Problem
算数のテストを受けることになった俺達は、今から勉強しても赤点を取ってしまうことを確信し、カンニングで乗り切ることを決意した。
算数のテスト問題を作成するA先生はテスト用紙を手書きで作ることで知られている。彼がテスト問題を作成している時の筆跡情報を、近所の博士に作ってもらった筆跡盗聴鉛筆で盗み取る作戦だ。だが肝心の筆跡情報から問題を復元するプログラムは博士の技術では作ることができなかった。しかも、たとえ問題が復元できたとしても、俺達の頭脳では問題を解くことができない。どうすることもできなくなった俺達は、プログラマーであるあなたに、筆跡情報から問題を復元し、それを解くプログラムの作成を依頼することにした。
今回のテストでは、数式を解く問題が出題される。数式中の演算記号は+(加算),-(減算),・(乗算)の3つのみで、乗算は加算、減算よりも優先して計算される。数式は必ず構文が正しいものが与えられる。また、0以外の数で、先頭が0であるものは与えられない。
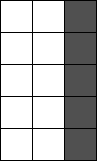
問題が書かれる紙はグリッドで表される。筆跡情報は線分の集合で与えられ、各線分はX軸に水平または垂直、もしくは始点、終点が同じ(点)である。この線分は、始点から終点までにあるマスを黒く塗りつぶすことを表す。座標(0, 0)が紙の左上である。数式の各文字(0,1,2,3,4,5,6,7,8,9,+,-,・)は以下で表される。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
 |
 |
 |
 |
 |
 |
 |
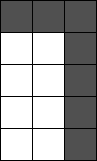
| 7 | 8 | 9 | + | - | ・ | |
 |
 |
 |
 |
 |
 |
A先生は印刷したかのような字を書くことで知られており、各文字は上記以外の書かれ方はしない。また、上記以外の文字が書かれることはない。2つ以上の文字がマスの辺を共有することはない。各文字の位置は、文字を構成するマス(黒いマス)の中で、最も左側にあるもののX座標で表される。数式の文字は、位置が小さい順に(左から右へ)解釈される。2つ以上の文字の位置が等しくなることはない。
Input
N X11 Y11 X12 Y12 X21 Y21 X22 Y22 : XN1 YN1 XN2 YN2
1行目に線分の数を表す1つの整数Nが与えられる。次に線分の情報がN行で与えられる。線分の情報のi行目には4つの整数Xi1, Yi1, Xi2, Yi2が空白区切りで与えられる。それぞれ、線分の1つ目の端点のX座標、Y座標、2つ目の端点のX座標、Y座標を表す。
Constraints
入力は以下の条件を満たす。
- 1 ≤ N ≤ 150
- 0 ≤ Xi1, Yi1, Xi2, Yi2 ≤ 200 (1 ≤ i ≤ N)
- Xi1 = Xi2 または Yi1 = Yi2 (1 ≤ i ≤ N)
- 計算の途中と結果に現れる数は符号付き32ビット整数に収まる
Output
各ケースの計算結果を一行に出力せよ。
Sample Input 1
4 1 1 1 5 3 3 5 3 4 2 4 4 7 1 7 5
Sample Output 1
2
Sample Input 2
23 1 1 3 1 3 1 3 3 3 3 1 3 1 3 1 5 1 5 3 5 5 2 7 2 7 2 7 4 7 4 5 4 5 4 5 6 5 6 7 6 11 4 13 4 13 0 15 0 15 0 15 4 18 2 18 2 21 5 23 5 21 5 21 7 21 7 23 7 23 7 23 9 23 9 21 9 24 0 26 0 24 0 24 4 24 4 26 4 26 0 26 4
Sample Output 2
-328
Hint
- 1つのグリッドを2度以上塗りつぶすことがある
- '1'など、1つの線分で表すことが可能でも、2つ以上の線分で表す場合がある

Sample Input 1の数式。

Sample Input 2の数式。"-7"の部分のように、ある文字を覆う最小の長方形の内部に別の文字が入り込む場合がある。